高中物理全反射计算题

如图所示，一个折射率为的三棱镜的截面为等腰直角△ABC，∠A为直角。此截面所在平面内的一束光线沿与AB边成θ角（θ＜90°）的方向入射到AB边的中点P处，若要光线进入三棱镜后能直接射到AC边上且能在AC面上发生全反射，则cosθ应满足什么条件？

1966年33岁的华裔科学家高锟首先提出光导纤维传输大量信息的理论，43年后高锟因此获得2009年诺贝尔物理学奖。如图所示，一长为L的直光导纤维，外套的折射率为n₁，内芯的折射率为n₂，一束单色光从图中O₁点进入内芯斜射到内芯与外套的介质分界面M点上恰好发生全反射，O₁O₂为内芯的中轴线，真空中的光速为c。求：

①该单色光在内芯与外套的介质分界面上发生全反射时临界角C的正弦值；
②该单色光在光导纤维中的传播时间。

如图所示，空气中有一横截面为半圆环的均匀透明柱体，其内圆半径为r，外圆半径为r。现有一束单色光垂直于端面A射入透明柱体，在柱体内恰好发生全反射，且只经过两次全反射就垂直于端面B射出。已知光在真空中的速度为c，求该光束在透明柱体内传播的时间。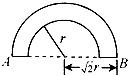

半径为R的半圆形玻璃砖截面如图所示，O点为圆心，光线a沿半径方向进入玻璃后恰好在O点发生全反射，光线b平行于光线a，从最高点进入玻璃后折射到MN上的D点，已知光线a与MN的夹角为60°，

求(1)玻璃的折射率n为多少？(2)OD的长度是多少？

国内最长的梅溪湖激光音乐喷泉，采用了世界一流的喷泉、灯光和音响设备，呈现出让人震撼的光与水的万千变化，喷泉的水池中某一彩灯发出的一条光线射到水面的入射角为，从水面上射出时的折射角是。
①求光在水面上发生全反射的临界角；
②在水池中m深处有一彩灯（看做点光源）。求这盏彩灯照亮的水面面积。

如图所示是一个半球形透明物体的侧视图，现在有一细束单色光沿半径OA方向入射，保持入射方向不变，不考虑光线在透明物体内部的反射。

（i）将细光束平移到距O点处的c点，此时透明体左侧恰好不再有光线射出，求透明体对该单色光的折射率；
（ii）若细光束平移到距O点0.5 R处，求出射光线与OA轴线的交点距O点的距离?

如图所示为一透明玻璃半球，在其下面有一平行半球上表面水平放置的光屏。两束关于中心轴OO＇对称的激光束从半球上表面垂直射入玻璃半球，恰能从球面射出。当光屏距半球上表面h₁=40cm时，从球面折射出的两束光线汇聚于光屏与OO＇轴的交点；当光屏距上表面h₂=70cm时，在光屏上形成半径R=40cm的圆形光斑。求光在该玻璃半球中的折射率n及玻璃半球的半径r.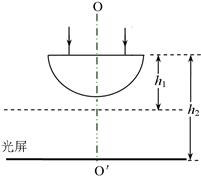

如图所示，一个横截面为直角三角形的三棱镜，∠A＝30°，∠C＝90°，三棱镜材料的折射率。一条与BC面夹角为的光线射向BC面，经过AC面一次反射，再从AB面射出，则从AB面射出的光线的折射角是多少？

如图所示，一个立方体玻璃砖的边长为a，折射率n=1.5，立方体中心有一个小气泡．为使从立方体外面各个方向都看不到小气泡，必须在每个面上都贴一张纸片，则每张纸片的最小面积为多少？

如图所示，1透明半圆柱体折射率为n=2，半径为R，长为L。平行光束从半圆柱体的矩形表面垂直射入，部分柱面有光线射出。求该部分柱面的面积S。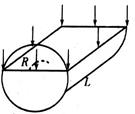

如图所示，半径为R的半圆柱形玻璃砖某一截面的圆心为O点。有两条光线垂直于水平柱面射入玻璃砖中，其中一条光线通过圆心O，另一条光线通过A点，且。这两条光线射出玻璃砖后相交于一点，该点到O点距离为R，求玻璃砖的折射率n

直角等腰玻璃三棱镜ABC的截面如图所示，∠ABC=∠ACB=45°，一条单色光线从腰AB上的D点射入三棱镜，射入玻璃的折射角r=30°,折射光线传播到BC边的E点。已知该玻璃的折射率n=。

（1）求光线的入射角i；
（2）判断光线在E点能否发生全反射。

如图所示，三角形ABC为某透明介质的横截面，介质折射率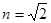，图中θ＝15⁰，O为BC的中点，位于截面所在平面内的一束光线自O点以i角入射，第一次到达AB边恰好发生全反射。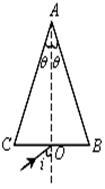

（1）求入射角i；
（2）通过计算判断光线能否在AC面上发生全反射？

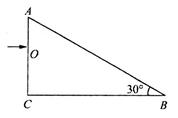
如图所示，直角三棱镜折射率为，∠B=30°，一束单色光垂直于AC面射向棱镜，入射点为O，试画出光在棱镜中传播的光路图，并求出光射出棱镜时折射角。(不考虑BC面对光线的反射)

如图所示，某同学用插针法测定半圆形玻璃砖的折射率，按规范先后插入、、、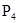四枚大头针后，移开玻璃砖作出分析图．用圆规以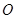点为圆心画一个圆，分别交入射光线和折射光线于A点和B点，量出这两点到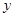轴的距离分别为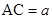、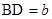，求: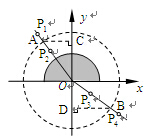

①玻璃砖的折射率；
②恰好发生全反射时临界角的正弦值．