高中物理光的折射定律综合题

如图13-1-13所示，一个人发现水中S处有一溺水者，溺水者离岸的距离SB="10" m，而发现者在A处，距B点的距离为20 m，此人在岸上跑动的速度为5 m/s，而在水中的速度为1 m/s,发现者为尽快到达溺水者处，他应在何处下水？

图13-1-13

如图13-1-9所示，一储油圆桶，底面直径与桶高均为d，当桶内无油时，从某点A恰能看到桶底边缘上的某点B，当桶内油的深度等于桶高一半时，在A点沿AB方向看去，看到桶底上的C点，C、B相距d，由此可得油的折射率n为多少?光在油中传播的速度v为多少?（结果可用根式表示）.

图13-1-9

如图13-1-7所示，光线从空气射入某液体中，入射角为45°，折射角为30°，光线射到液体底部水平放置的平面镜上反射回来，最后光线又回到空气中，这时折射角多大？

图13-1-7

如图10所示，在清澈平静的水底，抬头向上观察，会看到一个十分有趣的景象：
（1）水面外的景物（蓝天、白云、树木、房屋）都呈现在顶角为的倒立圆锥底面的“洞”内，设光在水中的临界角C=48.5°，求值是多少？
（2）试分析“洞”外是水底的镜像的原因；
（3）“洞”边呈彩色，试分析各种色光排列的顺序。

如图所示，半圆玻璃砖的半径R=10cm，折射率为n=，直径AB与屏幕垂直并接触于A点．激光a以入射角i=30°射向半圆玻璃砖的圆心O，结果在水平屏幕MN上出现两个光斑．求两个光斑之间的距离L．

在水面上放置一个足够大的遮光板，板上有一个半径为r的圆孔，圆心的正上方h 处放一个点光源S，在水面下深H处的底部形成半径为R的圆形光亮区域(图中未画出)．测得r=8cm，h=6cm，H=24cm，R=26cm，求水的折射率．

光线从空气射入玻璃砖，当入射角为60时，折射光线与发射光线恰好垂直。求：
①该玻璃砖的折射率是多少？ 
②光在该玻璃砖中传播速度是多少？ 

一个储油桶的底面直径与高均为d。当桶内没有油时，从某点A恰能看到桶底边缘的某点B，如图(a)所示，当桶内油的深度等于桶高的一半时，仍沿AB方向看去,恰好看到桶底上的点C，如图（b)所示，C、B两点相距d/4， (, .) 求

(1)试在图(b)中画出光路的示意图；
(2)油的折射率；
(3)光在油中传播的速度。

如图所示，一立方体玻璃砖放在空气中，平行光束从立方体的顶面斜射入玻璃砖，然后投射到它的一个侧面．若全反射临界角为42°，问：
(1)这光线能否从侧面射出？
(2)若光线能从侧面射出，玻璃砖的折射率应满足何条件？

如图所示，一点光源S放在10cm厚的玻璃板下面，在上面可看到一个圆形光斑，若玻璃折射率为1.5，请求出圆形光斑的直径为多少？

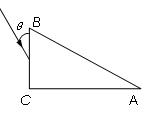
如图所示，一个横截面为直角三角形的三棱镜，ÐA=30°，ÐC＝90°．三棱镜材料的折射率是 n=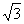。一条与BC面成θ＝30°角的光线射向BC面，经过AC边一次反射从AB边射出。求从AB边射出光线与AB边的夹角。(要作图并有计算过程)

如图所示，真空中有一个半径为R，折射率为n=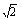的透明玻璃球.一束光沿与直径成θ₀=45°角的方向从P点射入玻璃球，并从Q点射出，求光线在玻璃球中的传播时间.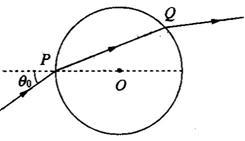

如图所示，玻璃三棱镜对红光的折射率为n₁，对紫光的折射率为n₂，三棱镜的AB面与屏平行，相距为d，三棱镜顶角A为，一束极细的白光由棱镜的一个侧面A垂直射入，通过棱镜从AB面射出，射在屏上形成彩色光带，求彩色光带的宽度。

如图所示，一束激光垂直照射在半球形玻璃砖的直径上，并过圆心O沿直线在球面上射出，玻璃砖的半径为R．当激光束向上平移距离d时，从A点垂直射入玻璃砖，恰好没有光线从球面上射出，求玻璃砖的折射率。 
                             

如图所示，ABC是由折射率为的某种透明物质制成的直角三棱镜横截面（O为AB的中点），∠A=30°，则：

（1）平行光束以α=45°的入射角自AB边折射进入棱镜后，请作出可能存在的典型光路图．（垂直于界面的反射光线不必画出）
（2）作图分析并计算要使射入O点的光线能从AC面射出，夹角α（如图所示）应满足什么条件？结果可用反三角函数表示。