高中物理光的折射定律试题

如图所示，将一等腰直角棱镜ABC截去棱角ADE，使其截面DE平行于底面BC，可制成“道威棱镜”，这样就减小了棱镜的重量和杂散的内部反射。已知棱镜玻璃的折射率n＝，棱边长cm，cm，一束平行于底边BC的单色光从DE边上的M点射入棱镜，求：

（i）光线进入“道威棱镜”时的折射角；
（ii）通过计算判断光线能否从BC边射出；
（ⅲ）光线在棱镜中传播所用的时间。

一束由红、蓝两单色光组成的光以入射角由空气射到半圆形玻璃砖表面的A处，AB是半圆的直径。进入玻璃后分为两束，分别为AC、AD，它们从A到C和从A到D的时间分别为和，则

A.AC是蓝光，小于      B.AC是红光，小于
C.AC是蓝光，等于       D.AC是红光，大于

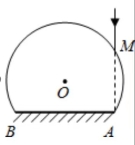
如图所示，一玻璃球体半径为R，O为球心，AD为水平直径。来自A点的单色光从B点射出，出射光平行于AD。已知玻璃对此光的折射率为。若真空中光的传播速度为c，求此光从A到B的传播时间t。

图示是一透明的圆柱体的横截面，其半径R=2cm，折射率．真空中一束光线沿平行于直径AB的方向从D点射入该透明体，折射光线恰好通过B点．已知真空中光速c=3.0×10⁸m/s，求：

①光在透明体中的传播速度v．
②入射点D与AB间的距离d．

如图所示，MN为竖直放置的光屏，光屏的左侧有半径为R、折射率为的透明半球体，O为球心，轴线OA垂直于光屏，O至光屏的距离OA=R，位于轴线上O点左侧R/3处的点光源S发出一束与OA夹角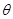=60°的光线射向半球体，求光线从S传播到达光屏的所用的时间。（已知光在真空中传播的速度为c）

某可见光在真空中波速为c，在水中波长为λ，频率为f，则该光在真空中的波长为       ，水对该光的折射率为      。若用该光在空气中进行双缝干涉实验，双缝间距为d，屏到双缝的距离为L，则屏上相邻两暗条纹间的距离为        。

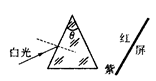
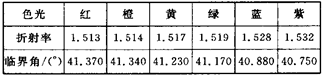
如图，一个棱镜的顶角为=41.30，一束白光以较大的入射角从棱镜的左侧面射入，在光屏上形成从红到紫排列的彩色光带，各色光在棱镜中的折射率和临界角见表．当入射角逐渐减小到0的过程中，彩色光带的变化情况是（ ）

A．紫光最先消失，最后只剩红光、橙光

B．紫光最先消失，最后只剩红光、橙光、黄光

C．红光最先消失，最后只剩紫光

D．红光最先消失，最后只剩紫光、蓝光

如图所示，OBCD为半圆柱体玻璃的横截面，OD为直径，一束由红光和紫光组成的复色光沿AO方向从真空斜射入玻璃，B、C点为两单色光的射出点(设光线在B、C处未发生全反射)。已知从B点射出的单色光由O到B的传播时间为t。

①若OB、OC两束单色光在真空中的波长分别为λ_B、λ_C，试比较λ_B、λ_C的大小(不必说明理由)；
②求从C点射出的单色光由O到C的传播时间t_C

如图所示，一个半径为R、折射率为的透明玻璃半球体，O为球心，轴线OA水平且与半球体的左边界垂直，位于轴线上O点左侧处的点光源S发出一束与OA夹角θ=60°光线射向半球体；已知光在真空中传播的速度为c，求：光线第一次从玻璃半球体出射时的方向以及光线在玻璃半球内传播的时间．

（1）由波源S形成的简谐横波在均匀介质中向左、右传播。波源振动的频率为20 Hz，波速为16 m/s。已知介质中P、Q两质点位于波源S的两侧，且P、Q和S的平衡位置在一条直线上，P、Q的平衡位置到S的平衡位置之间的距离分别为15．8 m、14．6 m，P、Q开始震动后，下列判断正确的是_____。

A．	P、Q两质点运动的方向始终相同
B．	P、Q两质点运动的方向始终相反
C．	当S恰好通过平衡位置时，P、Q两点也正好通过平衡位置
D．	当S恰好通过平衡位置向上运动时，P在波峰
E．	当S恰好通过平衡位置向下运动时，Q在波峰

（2）如图，玻璃球冠的折射率为 $\sqrt{3}$ ，其底面镀银，底面的半径是球半径的 $\frac{\sqrt{3}}{2}$ 倍；在过球心O且垂直于底面的平面（纸面）内，有一与底面垂直的光线射到玻璃球冠上的M点，该光线的延长线恰好过底面边缘上的A点。求该光线从球面射出的方向相对于其初始入射方向的偏角。

双缝干涉实验装置的截面图如图所示。光源 $S$ 到 $S_1$ 、 $S_2$ 的距离相等， $O$ 点为 $S_1$ 、 $S_2$ 连线中垂线与光屏的交点。光源 $S$ 发出的波长为 $\lambda$ 的光，经 $S_1$ 出射后垂直穿过玻璃片传播到 $O$ 点，经 $S_2$ 出射后直接传播到 $O$ 点，由 $S_1$ 到 $O$ 点与由 $S_2$ 到 $O$ 点，光传播的时间差为△ $t$ ．玻璃片厚度为 $10\lambda$ ，玻璃对该波长光的折射率为1.5，空气中光速为 $c$ ，不计光在玻璃片内的反射。以下判断正确的是 $($ 　　 $)$

A．

△ $t=\frac{5\lambda }{c}$

B．

△ $t=\frac{15\lambda }{2c}$

C．

△ $t=\frac{10\lambda }{c}$

D．

△ $t=\frac{15\lambda }{c}$

如图所示，横截面为直角三角形的玻璃砖ABC，AC边长为L，，光线P、Q同时由AC中点射入玻璃砖，其中光线P方向垂直AC边，光线Q方向与AC边夹角为，发现光线Q第一次到达BC边后垂直BC边射出，光速为c，求：

①玻璃砖的折射率；
②光线P由进入玻璃砖到第一次由BC边出射经历的时间

如图所示，在桌面上方有一倒立的玻璃圆锥，顶角∠AOB＝120°，顶点O与桌面的距离为4a，圆锥的底面半径R＝a，圆锥轴线与桌面垂直，有一半径为R的圆柱形平行光垂直入射到圆锥的底面上，光束的中心轴与圆锥的轴重合．已知玻璃的折射率n＝，求光束在桌面上形成的光斑的面积．

在真空中有一正方体玻璃砖，其截面如图所示，已知它的边长为d，玻璃砖的折射率n ＝，在AB面上方有一单色点光源S，从S发出的光线SP以60°入射角从AB面中点射入，从侧面AD射出，若光从光源S到AB面上P点的传播时间和它在玻璃砖中传播的时间相等．求点光源S到P点的距离

某种光学元件由两种不同透明物质I和透明物质II制成，其横截面如图所示，0为AB中点，∠BAC=30°，半圆形透明物质I的折射率为n₁=，透明物质Ⅱ的折射率为n₂。一束光线在纸面内沿O点方向射入元件，光线与AB面垂线间的夹角为，通过观察发现此时从AC面恰好无光线射出，在BC面有光线垂直射出。求：

①该透明物质Ⅱ的折射率n₂；
②光线在透明物质Ⅱ中的传播速度大小；
③光线与AB面垂线间的夹角的正弦值。