如图为一列沿x轴负方向传播的简谐横波在t=0时的波形图,当Q点在t=0时的振动状态传到P点时,则
| A.2 cm<x<3 cm范围内的质点正在向y轴的负方向运动 |
| B.Q处的质点此时的加速度沿y轴的负方向 |
| C.Q处的质点此时正在波谷位置 |
| D.Q处的质点此时运动到P处 |
一列简谐横波沿x轴正方向传播,图甲是t=3 s时的波形图,图乙是波中某质点P振动位移随时间变化的振动图线(两图用同一时间起点),下列判断正确的是
| A.质点P在t=3 s时正向y轴负方向振动 |
| B.质点P在t=3 s时的速度为零 |
| C.质点P的平衡位置可能是x=0 |
| D.质点P的平衡位置可能是x=2 m |
如图所示的实线是t=0时刻的波形图像,虚线是经过0.2 s时的波形图像.求:
(1)这列波可能的波速;
(2)若波速是35 m/s,求波的传播方向.
如图所示,一列简谐横波在x轴上传播,图甲和图乙分别为x轴上a、b两质点的振动图象,且xab=6 m.下列判断正确的是( )

| A.波长可能是8 m |
| B.波长可能是10 m |
| C.波速可定是1.2 m/s |
| D.波速可能是3.6m/s |
一列横波如图所示,波长λ=8 m,实线表示t1=0时刻的波形图,虚线表示t2=0.005 s时刻的波形图.则:
(1)波速可能多大?
(2)若波沿x轴负方向传播且2T>t2-t1>T,波速又为多大?
如图所示,两列简谐横波分别沿x轴正方向和负方向传播,两波源分别位于x=-0.2m和x=1.2m处,两列波的速度均为v=0.4m/s,两列波的振幅均为A=2cm.图示为t=0时刻两列波的图象(传播方向如图所示),此刻平衡位置处于x=0.2m和x=0.8m的P、Q两质点刚开始振动。质点M的平衡位置处于x=0.5m处,关于各质点运动情况判断正确的是( )
| A.t=1s时刻,质点M的位移为-4cm |
| B.t=1s时刻,质点M的位移为4cm |
| C.t=0.75s时刻,质点P、Q都运动到M点 |
| D.质 点P、Q的起振方向都沿y轴负方向 |
一列简谐横波向右传播,在其传播路径上每隔L="0.1" m选取一个质点,如图甲所示,t=0时刻波恰传到质点1,并立即开始向上振动,经过时间∆t="0.3" s,所选取的1-9号质点第一次出现如图乙所示的波形,则该波的( )
| A.周期为0.3 s,波长为0.8 m | B.周期为0.2 s,波长为0.9 m |
| C.周期为0.2 s,波速为4 m/s | D.周期为0.3 s,波速为2.67 m/s |
如图所示。甲为沿x轴传播的一列简谐横波在t=0时刻的波动图象,乙图为参与波动质点P的振动图象,则下列判断正确的是( )
| A.该波的传播速率为4 cm/s |
| B.该波的传播方向沿x轴正方向 |
| C.经过0.5s时间,质点P沿波的传播方向向前传播2 m |
| D.该波在传播过程中若遇到3 m的障碍物,能发生明显衍射现象 |
如图所示,波沿x轴正方向传播,质点p的坐标x=0.32 m.从此时刻开始计时.
(1)若每间隔最小时间0.4 s重复出现波形图,求波速.
(2)若p点经0.4 s第一次达到正向最大位移,求波速.
(3)若p点经0.4 s到达平衡位置,求波速.
如图所示,实线是沿x轴传播的一列简谐横波在t=0时刻的波形图,质点P恰好在平衡位置,虚线是这列波在t=0.8s时刻的波形图。已知该波的波速是3m/s,则下列说法正确的是
| A.这列波可能是沿x轴正方向传播的 |
| B.t=0.8s时,x=1.8m处的质点速度沿y轴负方向 |
| C.质点P在0.95s时的位移为2cm |
| D.质点P在1.0s时刻速度方向与加速度方向相同 |
如图所示,甲图为某波源的振动图象,乙图是该波源产生的横波在某时刻的波形图,波动图的O点表示波源.问:
(1)这列波的波速多大?
(2)若波向右传播,当波动图中质点Q第一次到达平衡位置且向上运动时,从乙图图示时刻开始质点P已经经过了多少路程?
一列沿x轴正方向传播的简谐横波在t=0时刻的波形如图所示,已知波的传播速度v=2m/s。
⑴写出从t=0时刻起x=2.0m处质点的位移y随时间t变化的表达式;
⑵求出在0~4.5s内波传播的距离及x=2.0m处质点通过的路
一简谐横波以4m/s的波速沿x轴正方向传播.已知t=0时的波形如图,则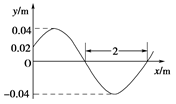
A.x=0处的质点在t=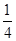 s时速度为0 s时速度为0 |
| B.波的周期为1 s |
| C.x=0处的质点在t=0时向y轴负向运动 |
D.x=0处的质点在t=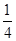 s时速度值最大 s时速度值最大 |
如图所示,沿x轴正方向传播的一列简谐横波在某时刻的波形图为一正弦曲线,其波速为200m/s,下列说法中正确的是
| A.质点b比质点a先回到平衡位置 |
| B.从图示时刻开始,质点b的速度将增大 |
| C.从图示时刻开始,质点b的加速度将增大 |
| D.从图示时刻开始,经过0.02 s,质点a向右迁移为4 m |