一理想变压器原、副线圈匝数比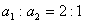 ,原线圈与正弦交变电源连接,输入电压u随时间t变化的规律如图所示,副线圈接一个R=10Ω的电阻,则()
,原线圈与正弦交变电源连接,输入电压u随时间t变化的规律如图所示,副线圈接一个R=10Ω的电阻,则()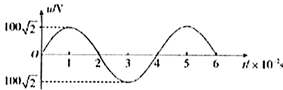
A.电阻R两端电压的有效值为50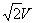 |
| B.电阻R中电流的频率为0.25Hz |
| C.1分钟内电阻R产生的热量为1.5-3J |
| D.变压器的输入功率为250W |
有一个电子器件,当其两端电压高于100 V时导电,等于或低于100 V时则不导电,若把这个电子器件接到100 V、50 Hz的正弦交流电源上,这个电子器件将( )
| A.不导电 |
| B.每秒钟导电50次 |
| C.每秒钟内导电100次 |
| D.每次导电的时间为0.005 s |
如图,理想变压器原副线圈匝数之比为2 : 1.原线圈接入一电压为 U=U0sinωt的交流电源,副线圈接一个R="55" Ω的负载电阻.若 U0=220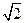 V ,ω="100π" rad/s , 则下述结论正确的是()
V ,ω="100π" rad/s , 则下述结论正确的是()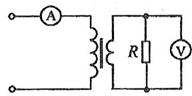
A.副线圈中电压表的读数为 110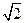 V V |
| B.副线圈中输出交流电的周期为0.02s |
| C.原线圈中电流表的读数为2A |
| D.原线圈中的输入功率为220W |
正弦交变电源与电阻R、交流电压表按照图甲所示的方式连接,R=10 Ω,交流电压表的示数是10 V.图乙是交变电源输出电压u随时间t变化的图象,则( )
A.通过R的电流iR随时间t变化的规律是iR= cos100πt(A)
cos100πt(A)
B.通过R的电流iR随时间t变化的规律是iR= cos50πt(A)
cos50πt(A)
C.R两端的电压uR随时间t变化的规律是uR=5 cos100πt(V)
cos100πt(V)
D.R两端的电压uR随时间t变化的规律是uR=5 cos50πt(V)
cos50πt(V)
如图所示,为一交流发电机和外接负载的示意图,发电机电枢线圈为n匝的矩形线圈,边长 = L1,
= L1, = L2,绕OO′轴在磁感强度为B的磁场中以角速度ω转动(不计一切摩擦),线圈电阻为r ,外电路负载电阻为R 。试求:
= L2,绕OO′轴在磁感强度为B的磁场中以角速度ω转动(不计一切摩擦),线圈电阻为r ,外电路负载电阻为R 。试求:
(1)电路中伏特表的示数;
(2)线圈每转动一周,外力所做的功。
..(15分)如图甲所示,一固定的矩形导体线圈水平放置,线圈的两端接一只小灯泡,在线圈所在空间内存在着与线圈平面垂直的均匀分布的磁场.已知线圈的匝数n=100匝,电阻r=1.0 Ω,所围成矩形的面积S=0.040 m2,小灯泡的电阻R=9.0 Ω,磁场的磁感应强度按如图12乙所示的规律变化,线圈中产生的感应电动势的瞬时值表达式为e=nBmScos(t),其中Bm为磁感应强度的最大值,T为磁场变化的周期.不计灯丝电阻随温度的变化,求:
(1)线圈中产生的感应电动势的最大值;
(2)小灯泡消耗的电功率;
(3)在磁感应强度变化的0~的时间内,通过小灯泡的电荷量.
下列说法正确的是()
| A. | 正弦交变电流的有效值是最大值的 倍 |
| B. | 声波是纵波,声源振动越快,声波传播也越快 |
| C. | 在某介质中,红光折射率比其他色光的小,故红光传播速度比其他色光的大 |
| D. | 质子和 粒子以相同速度垂直进入同一匀强磁场,质子做圆周运动的半径较小 |
如图所示,导体棒ab两个端点分别搭接在两个竖直放置、电阻不计、半径相等的金属圆环上,圆环通过电刷与导线c、d相接.c、d两个端点接在匝数比n1:n2=10:1的变压器原线圈两端,变压器副线圈接一滑动变阻器R0.匀强磁场的磁感应强度为B,方向竖直向下,导体棒ab长为l(电阻不计),绕与ab 平行的水平轴(也是两圆环的中心轴)OO'以角速度ω匀速转动。如果变阻器的阻值为R时,通过电流表的电流为I,则 
| A.变阻器上消耗的功率为P=10I2R |
| B.变压器原线圈两端的电压U1="10IR" |
C.取ab在环的最低端时t=0,则棒ab中感应电流的表达式是 |
D.ab沿环转动过程中受到的最大安培力F= BIl BIl |
如图甲所示,长、宽分别为L1、L2的矩形金属线框位于竖直平面内,其匝数为n,总电阻为r,可绕其竖直中心轴O1O2转动。线框的两个末端分别与两个彼此绝缘的铜环C、D(集流环)焊接在一起,并通过电刷和定值电阻R相连。线框所在空间有水平向右均匀分布的磁场,磁感应强度B的大小随时间t的变化关系如图乙所示,其中B0、B1和t1均为已知。在0~t1的时间内,线框保持静止,且线框平面和磁场垂直;t1时刻后线框在外力的驱动下开始绕其竖直中心轴以角速度ω匀速转动。求:
(1)0~t1时间内通过电阻R的电流大小;
(2)线框匀速转动后,在转动一周的过程中电流通过电阻R产生的热量;
(3)线框匀速转动后,从图甲所示位置转过90°的过程中,通过电阻R的电荷量。
一个半径r=0.10m的闭合导体圆环,圆环单位长度的电阻R0=1.0×10﹣2Ω/m.如图a所示,圆环所在区域存在着匀强磁场,磁场方向垂直圆环所在平面向外,磁感应强度大小随时间变化情况如图b所示.
(1)分别求在0~0.3s和0.3s~0.5s 时间内圆环中感应电动势的大小;
(2)分别求在0~0.3s和0.3s~0.5s 时间内圆环中感应电流的大小,并在图c中画出圆环中感应电流随时间变化的i﹣t图象(以线圈中逆时针电流为正,至少画出两个周期);
(3)求出导体圆环中感应电流的有效值.
在“练习使用示波器”实验中,某同学将衰减调节旋钮置于最右边的“∞”挡,扫描范围旋钮置于“外X”档,“X输入”与“地”之间未接信号输入电压,他在示波器荧光屏上看到的图象可能是下图中的()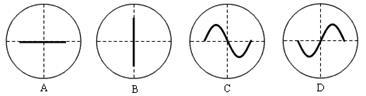
在匀强磁场中,一矩形金属线框绕与磁感线垂直的转动轴匀速转动,如图甲所示。产生的交变电动势随时间变化的规律如图乙所示。则下列说法正确的是() 
| A.t=0.01s时穿过线框的磁通量最小 |
B.该交变电动势的有效值为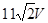 |
C.该交变电动势的瞬时值表达式为 |
| D.电动势瞬时值为22V时,线圈平面与中性面的夹角为45° |
在匀强磁场中匀速转动的矩形线圈的周期为T,转轴 垂直于磁场方向,线圈电阻为2Ω,从线圈平面与磁场方向平行时开始计时,线圈转过了60°的感应电流为1A,那么
垂直于磁场方向,线圈电阻为2Ω,从线圈平面与磁场方向平行时开始计时,线圈转过了60°的感应电流为1A,那么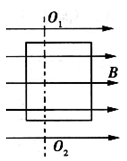
| A.线圈中感应电流的有效值为2A |
| B.线圈消耗的电功率为4W |
C.任意时刻线圈中的感应电动势为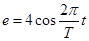 |
D.任意时刻穿过线圈的磁通量为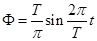 |
有一个电热器,工作时的电阻为50 ,接在电压
,接在电压 (V)的交流电源上,求:
(V)的交流电源上,求:
(1)该电热器两端电压的有效值;
(2)该电热器消耗的电功率;
(3)10s 时间内电热器中的电流方向发生改变的次数。