某小组同学利用磁传感器探究通电螺线管轴线上不同位置的磁感应强度,如图甲所示.将传感器探头沿螺线管轴线移动时,测得磁感应强度B的大小随位置x的变化关系如图乙所示.图乙中a、b两点对应位置分别处在( )
| A.螺线管内、螺线管内 | B.螺线管内、螺线管外 |
| C.螺线管外、螺线管外 | D.螺线管外、螺线管内 |
下列说法正确的是( )
| A.磁场中某处磁感强度的大小,等于长为L,通以电流I的一小段导线放在该处时所受磁场力F与乘积IL的比值. |
| B.一小段通电导线放在某处如不受磁场力作用,则该处的磁感应强度为零. |
| C.因为B=F/IL,所以磁场中某处磁感应强度的大小与放在该处的导线所受磁场力F的大小成正比,与IL的大小成反比. |
| D.磁场中某处磁感应强度的大小与放在磁场中的通电导线长度、电流大小及所受磁场力的大小均无关. |
下列说法中正确的是( )
| A.点电荷就是体积和带电荷量都很小的带电体 |
B.根据F= ,当r→0时,可得出F→∞ ,当r→0时,可得出F→∞ |
C.由 可知,某处的磁感应强度的大小与放入该处的通电导线所受磁场力F成正比,与导线的I、L成反比 可知,某处的磁感应强度的大小与放入该处的通电导线所受磁场力F成正比,与导线的I、L成反比 |
| D.一小段通电导体在磁场中某处不受磁场力作用,该处磁感应强度不一定为零 |
关于电场线和磁感线的概念,以下说法中正确的是( )
| A.电场线和磁感线都是不封闭的曲线 |
| B.沿着磁感线的方向,磁场越来越弱 |
| C.任意两条电场线或磁感线都不能相交 |
| D.电场线和磁感线的疏密都表示场的强弱 |
下列物理量在运算时遵循平行四边形定则的是
| A.电流强度 | B.电场强度 | C.磁通量 | D.磁感应强度 |
如图是几种常见磁场的磁感线分布示意图,下列说法正确的是( )

| A.图(a)中a端是磁铁的S极,b端是磁铁的N极 |
| B.图(a)中a端是磁铁的N极,b端是磁铁的S极 |
| C.图(b)是两异名磁极的磁感线分布示意图,c端是N极,d端是S极 |
| D.图(b)是两异名磁极的磁感线分布示意图,c端是S极,d端是N极 |
两条金属导轨上水平放置一根导电棒ab,处于竖直向上的匀强磁场中,如图所示,导电棒质量为1.2kg,长1m。当导电棒中通入3A电流时,它可在导轨上匀速滑动,若电流强度增大为5A时,导电棒可获得2m/s2的加速度,求装置所在处的磁感强度的大小。
如图10所示,正方形线框ABCD的总电阻R为0.4Ω,质量m为0.1kg,边长为0.4m,两虚线之间是垂直于线框平面向里的匀强磁场,磁场上限(上面一条虚线)正好过AC和BD的中点,磁感应强度从2T开始以5T/s的变化率均匀增大,当磁感应强度为多大时,悬线的拉力为零?(AB边水平)
把一根长l = 10cm的导线垂直磁感线方向放入如图所示的匀强磁场中,
(1)当导线中通以I1 = 2A的电流时,导线受到的安培力大小为1.0×10-7N,则该磁场的磁感应强度为多少?
(2)若该导线中通以I2 = 3A的电流,则此时导线所受安培力大小是多少?方向如何?
所示为一块霍尔元件,其横载面为矩形,霍尔元件的长、宽、高分别为c、b、d。已知其单位体积内的电子数为n、电子电荷量e.将此元件放在匀强磁场中,磁场方向沿Z轴方向,并通有沿x轴方向的电流I。
试证明在磁感应强度为定值B时,稳定后此元件的 两个侧面的电势差
两个侧面的电势差
水平面上两根足够长的金属导轨平行固定放置,间距为L,一端通过导线与阻值为R的电阻连接;导轨上放一质量为m的金属杆(如图1(a)所示),金属杆与导轨的电阻忽略不计。均匀磁场竖直向下,用与导轨平行的恒定拉力F作用在金属杆上,杆最终将做匀速运动。当改变拉力的大小时,相对应的匀速运动速度v也会变化,v和F的关系如图1(b)所示(取重力加速度 ):
):
(1)若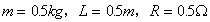 ;则磁感应强度B为多大?
;则磁感应强度B为多大?
(2)由 图线的截距可求得什么物理量?其值为多少?
图线的截距可求得什么物理量?其值为多少?
在赤道附近的地磁场可看做是沿南北方向的匀强磁场,磁感应强度的大小是0.5×10-4T。如果赤道上有一根沿东西方向的直导线,长20m,通有从东向西的电流30A,问地磁场对这根导线的作用力有多大?方向如何?
在倾角为α的光滑斜面上,放置一个通有电流为I、长为L、质量为m的导体棒,如图所示,求:
(1)欲使棒静止在斜面上,外加匀强磁场的磁感应强度B的最小值和方向。
(2)欲使棒静止在斜面上且对斜面无压力,外加匀强磁场的磁感应强度B的大小和方向