高中物理电荷守恒定律试题

如图所示，光滑水平面上有一矩形长木板，木板左端放一小物块，已知木板质量大于物块质量，t=0时两者从图中位置以相同的水平速度v₀向右运动，碰到右面的竖直挡板后木板以与原来等大反向的速度被反弹回来，运动过程中物块一直未离开木板，则关于物块运动的速度v随时间t变化的图象可能正确的是

在如图所示的光滑水平面上，小明站在静止的小车上用力向右推静止的木箱，木箱以速度v向右匀速运动。巳知木箱的质量为m．人与车的质量为2m。木箱运动一段时间后与竖直墙壁发生无机械能损失的碰撞，反弹回来后被小明接住。求：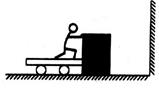

①推出木箱后小明和小车一起运动的速度v₁的大小；
②小明接住木箱后三者一起运动的速度v₂的大小。

某缓冲装置的理想模型如图所示，劲度系数足够大的轻质弹簧与轻杆相连，轻杆可在固定的槽内移动，与槽间的滑动摩擦力恒为f．轻杆向右移动不超过L时，装置可安全工作。轻杆与槽间的最大静摩擦力等于滑动摩擦力，且不计小车与地面的摩擦。一质量为m的小车若以速度v撞击弹簧，将导致轻杆向右移动。

（1）若弹簧的劲度系数为k，求轻杆开始移动时，弹簧的压缩量x
（2）若以速度v₀（已知）撞击，将导致轻杆右移，求小车与弹簧分离时速度（k未知）
（3）在(2)问情景下，求为使装置安全工作，允许该小车撞击的最大速度v_m（k未知）

如图所示，在光滑水平地面上，有一质量的平板小车，小车的右端有一固定的竖直挡板，挡板上固定一轻质细弹簧．位于小车上A点处的质量为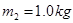的木块（视为质点）与弹簧的左端相接触但不连接，此时弹簧与木块间无相互作用力。木块与A点左侧的车面之间有摩擦，与A点右侧的车面之间的摩擦可忽略不计．现小车与木块一起以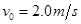的初速度向右运动，小车将与其右侧的竖直墙壁发生碰撞，已知碰撞时间极短，碰撞后小车以的速度水平向左运动，取．

①求小车与竖直墙壁发生碰撞的过程中小车动量变化量的大小；
②若弹簧始终处于弹性限度内，求小车撞墙后与木块相对静止时的速度大小和弹簧的最大弹性势能；

如图所示，两块相同平板P₁、P₂置于光滑水平面上，质量均为m。P₂的右端固定一轻质弹簧，弹簧的自由端恰好在P₂的左端A点。物体P置于P₁的最右端，质量为2m且可以看作质点。P₁与P以共同速度v₀向右运动，与静止的P₂发生碰撞，碰撞时间极短，碰撞后P₁与P₂粘连在一起，P压缩弹簧后被弹回并停在A点(弹簧始终在弹性限度内)。P与P₂之间的动摩擦因数为μ，求

①P₁、P₂刚碰完时的共同速度v₁和P的最终速度v₂；
②此过程中弹簧最大压缩量x。

如图所示，光滑平台上有两个刚性小球A和B，质量分别为2m和3m，小球A以速度v₀向右运动并与静止的小球B发生碰撞（碰撞过程不损失机械能），小球B飞出平台后经时间t刚好掉入装有沙子向左运动的小车中，小车与沙子的总质量为m，速度为2v₀，小车行驶的路面近似看做是光滑的，求：

（1）碰撞后小球A和小球B的速度；
（2）小球B掉入小车后的速度。

如图所示，水平地面上静止放置一辆小车A，质量m_A＝4 kg，上表面光滑，小车与地面间的摩擦力极小，可以忽略不计．可视为质点的物块B置于A的最右端，B的质量m_B＝2 kg.现对A施加一个水平向右的恒力F＝10 N，A运动一段时间后，小车左端固定的挡板与B发生碰撞，碰撞时间极短，碰后A、B粘合在一起，共同在F的作用下继续运动，碰撞后经时间t＝0.6 s，二者的速度达到v_t＝2 m/s.求：

(i)A开始运动时加速度a的大小；
(ii)A、B碰撞后瞬间的共同速度v的大小；
(iii)A的上表面长度l。

质量均为m="2" kg的三物块A、B、C，物块A、B用轻弹簧相连，初始时弹簧处于原长，A、B两物块都以v="3" m/s的速度在光滑的水平地面上运动，物块C静止在前方，如图所示。B与C碰撞后二者会粘在一起运动。求在以后的运动中：

(1)从开始到弹簧的弹性势能第一次达到最大时，弹簧对物块A的冲量；
(2)系统中弹性势能的最大值E_P是多少？

如图所示，光滑水平面上有A、B、C三个物块，其质量分别为m_A =2kg，m_B =1kg，m_C =1kg．现用一轻弹簧将A、B两物块连接，并用力缓慢压缩弹簧使A、B两物块靠近，此过程外力做功W=108J（弹簧仍处于弹性限度内），然后同时释放A、B，弹簧开始逐渐变长，当弹簧刚好恢复原长时，C恰以4m/s的速度迎面与B发生碰撞并粘连在一起．求：

①弹簧刚好恢复原长时（B与C碰撞前）A和B物块速度的大小？
②当弹簧第二次被压缩到最短时，弹簧具有的弹性势能为多少？

(9分)一质量为的子弹以某一初速度水平射入置于光滑水平面上的木块并留在其中，与木块用一根弹性良好的轻质弹簧连在一起，开始弹簧处于原长，如图所示。已知弹簧被压缩瞬间的速度，木块、的质量均为。求：

子弹射入木块时的速度；
‚弹簧被压缩到最短时弹簧的弹性势能。

如图所示，固定的光滑平台左端固定有一光滑的半圆轨道，轨道半径为R，平台上静止放着两个滑块A、B，其质量m_A=m，m_B =2m，两滑块间夹有少量炸药．平台右侧有一小车，静止在光滑的水平地面上，小车质量M=3m，车长L=2R，车面与平台的台面等高，车面粗糙，动摩擦因数μ=0.2，右侧地面上有一立桩，立桩与小车右端的距离为S，S在0<S<2R的范围内取值，当小车运动到立桩处立即被牢固粘连。点燃炸药后，滑块A恰好能够通过半圆轨道的最高点D，滑块B冲上小车．两滑块都可以看作质点，炸药的质量忽略不计，爆炸的时间极短，爆炸后两个滑块的速度方向在同一水平直线上，重力加速度为g=10m/s²．求：

（1）滑块A在半圆轨道最低点C受到轨道的支持力F_N。
（2）炸药爆炸后滑块B的速度大小v_B。
（3）请讨论滑块B从滑上小车在小车上运动的过程中，克服摩擦力做的功W_f与S的关系。

用下图实验装置来研究碰撞问题，用完全相同的轻绳将两个大小相同、质量相等的小球并列悬挂于一水平杆，球间有微小间隔．将1号球向左拉起，然后由静止释放，使其与2号球发生弹性正碰，不计空气阻力，忽略绳的伸长．下列说法正确的是( )

A．碰撞过程中两球构成的系统动量和机械能都守恒

B．碰撞过程中两球构成的系统动量和机械能都不守恒

C．碰撞过程中两球的速度互换

D．碰撞后两球以共同的速度向右摆

如图所示，一轻质弹簧两端连着物体A和B，放在光滑的水平面上，物体A被水平速度为v₀的子弹射中并且嵌入其中。已知物体B的质量为m，物体A的质量是物体B的质量的，子弹的质量是物体B的质量的，求

①弹簧压缩到最短时物体B的速度。
②弹簧的最大弹性势能。

如图所示，直角坐标系xOy位于竖直平面内，x轴与绝缘的水平面重合，在y轴右方有垂直纸面向里的匀强磁场和竖直向上的匀强电场．质量为m₂＝8×10^－3 kg的不带电小物块静止在原点O，A点距O点l＝0.045 m，质量m₁＝1×10^－3 kg的带电小物块以初速度v₀＝0.5 m/s从A点水平向右运动，在O点与m₂发生正碰并把部分电量转移到m₂上，碰撞后m₂的速度为0.1 m/s，此后不再考虑m₁、m₂间的库仑力。已知电场强度E＝40 N/C，小物块m₁与水平面的动摩擦因数为μ＝0.1，取g＝10 m/s²，求：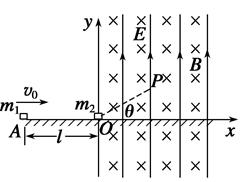

(1)碰后m₁的速度；
(2)若碰后m₂做匀速圆周运动且恰好通过P点，OP与x轴的夹角θ＝30°，OP长为l_OP＝0.4 m，求磁感应强度B的大小；
(3)其他条件不变，若改变磁场磁感应强度B′的大小，使m₂能与m₁再次相碰，求B′的大小。

如图，质量为M的小车A停放在光滑的水平面上，小车上表面粗糙。质量为m的滑块B以初速度v₀滑到小车A上，车足够长，滑块不会从车上滑落，则小车的最终速度大小为________（填选项前的字母）

A．零

B．

C．

D．