高中物理封闭气体压强计算题

有一传热良好的圆柱形气缸置于水平地面上，并用一光滑的质量为M活塞密封一定质量的的理想气体，活塞面积为S。开始时汽缸开口向上（如图一），已知外界大气压强P₀，被封气体的体积V₀。

①求被封气体的压强：
②现将汽缸倒置（如图二），待系统重新稳定后，活塞移动的距离是多少？

如图所示，固定的绝热气缸内有一质量为m的“T”型绝热活塞（体积可忽略），距气缸底部h₀处连接一U形管（管内气体的体积忽略不计）。初始时，封闭气体温度为T₀，活塞距离气缸底部为1.5h₀，两边水银柱存在高度差。已知水银的密度为ρ，大气压强为p₀，气缸横截面积为S，活塞竖直部分长为1.2h₀，重力加速度为g。求：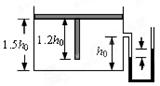

①初始时，水银柱两液面高度差。
②通过制冷装置缓慢降低气体温度，当温度为多少时两水银面相平。

如图，在柱形容器中密闭有一定质量气体，一具有质量的光滑导热活塞将容器分为A、B两部分，离气缸底部高为49cm处开有一小孔，与U形水银管相连，容器顶端有一阀门K．先将阀门打开与大气相通，外界大气压等于p₀=75cmHg，室温t₀=27°C，稳定后U形管两边水银面的高度差为△h=25cm，此时活塞离容器底部为L=50cm．闭合阀门，使容器内温度降至﹣57°C，发现U形管左管水银面比右管水银面高25cm．求：

（1）此时活塞离容器底部高度L′；
（2）整个柱形容器的高度H．

一定质量的理想气体从状态A变化到状态B，再变化到状态C，其状态变化过程的p-V图象如图所示。已知该气体在状态A时的温度为27℃。则：
（1）该气体在状态B、C时的温度分别为多少℃？
（2）该气体从状态A到状态C的过程中内能的变化量是多大？
（3）该气体从状态A到状态C的过程中是吸热，还是放热？传递的热量是多少？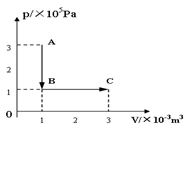

一定质量的理想气体由状态A经状态B变为状态C，其中A→B过程为等压变化，B→C过程为等容变化。已知V_A＝0.3 m³，T_A＝T_C＝300 K，T_B＝400 K。
⑴求气体在状态B时的体积；
⑵说明B→C过程压强变化的微观原因；
⑶设A→B过程气体吸收热量为Q₁，B→C过程气体放出热量为Q₂，比较Q₁、Q₂的大小并说明原因。

如图，竖直平面内有一直角形内径相同的细玻璃管，A端封闭，C端开口，AB=BC=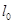，且此时A、C端等高。平街时，管内水银总长度为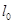，玻璃管AB内封闭有长为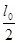的空气柱。已知大气压强为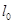汞柱高。如果使玻璃管绕B点在竖直平面内顺时针缓慢地转动至BC管水平，求此时AB管内气体的压强为多少汞柱高?管内封入的气体可视为理想气体且温度不变。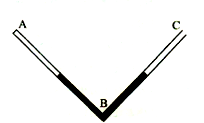

已知阿伏伽德罗常数为6.0×10²³mol^-1，在标准状态（压强p₀=1atm、温度t₀=0℃）下理想气体的摩尔体积都为22.4L，已知第（2）问中理想气体在状态C时的温度为27℃，求该气体的分子数（计算结果保留两位有效数字）．

如图所示，圆柱形气缸开口向上竖直放置在水平面上，气缸足够长，内截曲积为S,大气压强为P₀，一厚度不计、质量为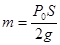的活塞封住一定量的理想气体，温度为T₀时缸内气体体积为V₀ ，先在活塞上缓慢放上质量为3m的砂子，然后将缸内气体温度缓慢升高到2T₀，求：

①最后缸内气体的体积；
②在右图中做出缸内气体状态变化的P-V图象

如图所示，在长为l="57" cm的一端封闭、另一端开口向上的竖直玻璃管内，用4 cm高的水银柱封闭着51 cm长的理想气体，管内外气体的温度相同。现将水银缓慢地注入管中，直到水银面与管口相平。(大气压强P₀=276cmHg)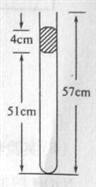

①求此时管中封闭气体的压强；
②此过程封闭气体     (填“吸热”或“放热”)，内能    (填“增大”、“减小”或“不变”)。

如图所示，粗细均匀的U形管竖直放置，左端封闭，右端开口，左端用水银封闭着长L＝10cm的理想气体，当温度为27°C时，两管水银面的高度差Δh＝2cm．设外界大气压为1.0´10⁵Pa（即75cmHg）．为了使左、右两管中的水银面相平，求：

若对封闭气体缓慢加热，温度需升高到多少°C？
若温度保持27°C不变，需从右管的开口端再缓慢注入多少高度的水银柱?

（1）关于空气湿度，下列说法正确的是           （填入正确选项前的字母。选对1个给2分，选对2个给4分；选错1个扣2分，最低得0分）。

A．当人们感到潮湿时，空气的绝对湿度一定较大

B．当人们感到干燥时，空气的相对湿度一定较小

C．空气的绝对湿度用空气中所含水蒸汽的压强表示

D．空气的相对湿度定义为水的饱和蒸汽压与相同温度时空气中所含水蒸气的压强之比

（2）如图，容积为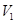的容器内充有压缩空气。容器与水银压强计相连，压强计左右两管下部由软胶管相连。气阀关闭时，两管中水银面等高，左管中水银面上方到气阀之间空气的体积为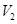。打开气阀，左管中水银下降；缓慢地向上提右管，使左管中水银面回到原来高度，此时右管与左管中水银面的高度差为h。已知水银的密度为，大气压强为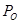，重力加速度为g；空气可视为理想气体，其温度不变。求气阀打开前容器中压缩空气的压强P₁。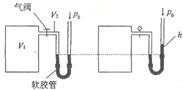

(10分)一气象探测气球，在充有压强为1.00 atm(即76.0 cmHg)、温度为27.0℃的氦气时，体积为3.50 m³.在上升至海拔6.50 km高空的过程中，气球内氦气压强逐渐减小到此高度上的大气压36.0 cmHg，气球内部因启动一持续加热过程而维持其温度不变．此后停止加热，保持高度不变．已知在这一海拔高度气温为－48.0℃.求：
(1)氦气在停止加热前的体积；
(2)氦气在停止加热较长一段时间后的体积．

如图12-6所示为一简易火灾报警装置。其原理是：竖直放置的试管中装有水银，当温度升高时，水银柱上升，使电路导通，蜂鸣器发出报警的响声。27℃时，空气柱长度L₁为20cm，水银上表面与导线下端的距离L₂为10cm，管内水银柱的高度h为8cm，大气压强为75cm水银柱高。
（1）当温度达到多少℃时，报警器会报警？
（2）如果要使该装置在87℃时报警，则应该再往玻璃管内注入多少cm高的水银柱？
（3）如果大气压增大，则该报警器的报警温度会受到怎样的影响？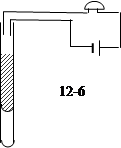

在气球内部充有压强为1.0atm(即76cmH_g)、温度为27⁰C的氦气时，其体积为3.5m³。在气球上升至海拔6.5km高空的过程中，气球内氦气的压强逐渐减小到此高度上的大气压38cmH_g，此过程中气球内部因为启动一个可持续加热装置，而保持球内温度不变，此后停止加热，保持气球高度不变，已知在这一海拔高度气温为零下33⁰C，设气球内外压强相等，不计气球的厚度。求：
（1）气球在停止加热前的体积
（2）在加热过程中，球内加热装置放热500J，气球放热20J，求气体对外界做的功
（3）氦气在停止加热较长一段时间后的气球体积

一足够高的直立汽缸上端开口，用一个厚度不计的活塞封闭了一段高为80 cm的气柱，活塞的横截面积为0.01 m²，活塞与汽缸间的摩擦不计，汽缸侧壁通过一个开口与U形管相连．开口离气缸底部的高度为70 cm，开口管内及U形管内的气体体积忽略不计，已知图13－2－14所示状态时气体的温度为7 ℃，U形管内水银面的高度差h₁＝5 cm，大气压强p₀＝1.0×10⁵ Pa保持不变，水银的密度ρ＝13.6×10³ kg/m³，g＝10 m/s².求：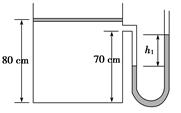

图13－2－14
(1)活塞的重力．
(2)现在活塞上添加砂粒，同时对汽缸内的气体加热，始终保持活塞的高度不变，此过程缓慢进行，当气体的温度升高到37℃时，U形管内水银面的高度差为多少？