弹簧振子以O点为平衡位置做简谐运动,从O点开始计时,振子第一次到达M点用了0.3 s时间,又经过0.2 s第二次通过M点,则振子第三次通过M点还要经过的时间可能是( )
A. s s |
B. s s |
C.1.4 s | D.1.6 s |
如图11-2-4所示,一个做简谐运动的质点,先后以同样大小的速度通过相距10 cm的A、B两点,历时0.5 s,过B点后再经过t="0.5" s质点以方向相反、大小相同的速度再次通过B点,则质点振动的周期是( )
图11-2-4
A.0.5 s B.1.0 s C.2.0 s D.4.0 s
做简谐运动的弹簧振子,振子质量为m,最大速度为v,则下列说法正确的是( )
| A.从某时刻算起,在半个周期的时间内,回复力做的功一定为零 |
B.从某时刻算起,在半个周期的时间内,回复力做的功可能是零到 mv2之间的某一个值 mv2之间的某一个值 |
| C.从某一时刻算起,在半个周期的时间内,速度变化量一定为零 |
| D.从某一时刻算起,在半个周期的时间内,速度变化量的大小可能是零到2v之间的某一值 |
如图11-3-7所示,一弹簧振子在A、B间做简谐运动,平衡位置为O,已知振子的质量为M,若振子运动到B处时将一质量为m的物体放在M的上面,且m和M无相对运动而一起运动,下述正确的是( )
图11-3-7
A.振幅不变 B.振幅减小
C.最大动能不变 D.最大动能减少
A.若t时刻和(t+△t)时刻振子运动速度的大小相等、方向相反,则Δt一定等于T/2的整数倍
D.若t时刻和(t+△t)时刻振子运动位移的大小相等、方向相同,则△t一定等于T的整数倍
C.若△t=T/2,则在t时刻和(t-△t)时刻弹簧的长度一定相等
D.若△t=T,则在t时刻和(t-△t)时刻振子运动的加速度一定相同
现有一波源,振动图像如图甲所示,在介质中传播时,波长为8d。现其振动 T便停止,则在t=
T便停止,则在t= T时在介质中形成的波形图是下列的哪一个:
T时在介质中形成的波形图是下列的哪一个:

如图所示,一个弹簧振子在A、B两点间做简谐运动,O点为平衡位置,下列说法中正确的有( )
A.它在A、B两点时动能为零
B.它经过O点时加速度方向要发生变化
C.它远离O点时作匀减速运动
D.它所受回复力的方向总跟它偏离平衡位置的位移方向相反
某地区地震波中的横波和纵波传播速率分别约为.一种简易地震仪由竖直弹簧振子
和水平弹簧振子
组成.在一次地震中,震源地地震仪下方,观察到两振子相差
开始振动,则()
| A. |
|
| B. |
|
| C. |
|
| D. |
|
弹簧振子在光滑的水平面上作简谐振动,周期是2.4s。当振子通过平衡位置向右运动时刻开始计时。有下列说法:①经过1.6s,振子向右运动,速度正在不断变小;②经过1.6s,振子向左运动,速度正在不断变小;③经过1.9s,振子向右运动,回复力正在不断变小;④经过1.9s,振子向左运动,回复力正在不断变大。以上说法中正确的是( )
| A.只有①、③正确 | B.只有②、④正确 |
| C.只有①、④正确 | D.只有②、③正确 |
如图所示。弹簧振子在振动过程中,振子经a、b两点的速度相同,若它从a到b历时0.2s,从b再回到a的最短时间为0.4s,则该振子的振动频率为:()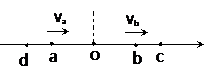
| A.1Hz; | B.1.25Hz; | C.2Hz; | D.2.5Hz。 |
弹簧振子在光滑的水平面上做简谐运动,在振子向平衡位置运动的过程中:
| A.振子所受的回复力逐渐增大 |
| B.振子的位移逐渐增大 |
| C.振子的速度逐渐减小 |
| D.振子的加速度逐渐减小。 |
如图所示,一轻质弹簧竖直放置,下端固定在水平面上,上端处于a位置,当一重球放在弹簧上端静止时,弹簧上端被压缩到b位置。现将重球(视为质点)从高于位置的c位置沿弹簧中轴线自由下落,弹簧被重球压缩到最低位置d。以下关于重球运动过程的正确说法应是
| A.重球下落压缩弹簧由a至d的过程中,重球做减速运动。 |
| B.重球下落至b处获得最大速度。 |
| C.重球下落至d处获得最大加速度。 |
| D.由a至d过程中重球克服弹簧弹力做的功等于小球由c下落至d处时重力势能减少量。 |
如图所示,S1、S2是两个相干波源,它们振动同步且振幅相同。实线和虚线分别表示在某一时刻它们所发出的波的波峰和波谷。关于图中所标的a、b、c、d四点,下列说法中正确的有
| A.该时刻a质点振动最弱,b、c质点振动最强,d质点振动既不是最强也不是最弱 |
| B.该时刻a质点振动最弱,b、c、d质点振动都最强 |
| C.a质点的振动始终是最弱的, b、c、d质点的振动始终是最强的 |
| D.再过T/4后的时刻a、b、c三个质点都将处于各自的平衡位置,因此振动最弱 |