将一个力传感器连接到计算机上，我们就可以测量快速变化的力。图中所示就是用这种方法测得的小滑块在半球形碗内在竖直平面内来回滑动时，对碗的压力大小随时间变化的曲线。从这条曲线提供的信息，可以判断滑块约每隔 秒经过碗底一次，随着时间的变化滑块对碗底的压力 （填“增大”、“减小”、“不变”或“无法确定”）。
A、B两个完全一样的弹簧振子，把A振子移到A的平衡位置右边10cm，把B振子移到B的平衡位置右边5cm，然后同时放手，那么：（ ）
A．A、B运动的方向总是相同的 B．A、B运动的方向总是相反的
C．A、B运动的方向有时相同、有时相反 D．无法判断A、B运动的方向的关系
如图所示，质量为m＝0.5kg的物体放在质量为M＝4.5kg的平台上，随平台上、下做简谐运动．设在简谐运动过程中，二者始终保持相对静止．已知弹簧的劲度系数为k＝400N/m，振幅为A＝0.1m. 试求：二者一起运动到最低点时，物体对平台的压力大小 (取g＝10m/s)
若物体做简谐运动，则下列说法中正确的是( )
| A．若位移为负值，则速度一定为正值，加速度也一定为正值 |
| B．物体通过平衡位置时，所受合外力为零，回复力为零，处于平衡状态 |
| C．物体每次通过同一位置时，其速度不一定相同，但加速度一定相同 |
| D．物体的位移增大时，动能增加，势能减少 |
如图所示，一弹簧振子在B、C间做简谐运动，O为平衡位置，BC间距离为10cm， 从B到C运动一次的时间为1s，则
| A．从B到C振子作了一次全振动 |
| B．振动周期为2s，振幅为5cm |
| C．经过两次全振动，振子通过的路程是20cm |
| D．振子从B点开始，经3s位移是30cm |
如图所示，质量为m的砝码A放置在质量为M的滑块B上，B与弹簧相连，它们一起在光滑的水平面上作简谐运动，弹簧的劲度系数为k，砝码与滑块之间的动摩擦因数为
，要使砝码与滑块在振动过程中不发生相对运动，问最大振幅等于多少？（设最大静摩擦力等于滑动摩擦力）
用两根完全一样的弹簧和一根细线将甲、乙两滑块连在光滑的水平面上．线上有张力，甲的质量大于乙的质量，如图所示．当线突然断开后，两滑块都开始做简谐运动，在运动过程中( )
| A．甲的振幅一定等于乙的振幅 |
| B．甲的振幅一定小于乙的振幅 |
| C．甲的最大速度一定大于乙的最大速度 |
| D．甲的最大速度一定小于乙的最大速度 |
如图所示，弹簧振子以点O为平衡位置，在A、B两点之间做简谐运动。取向右为正方向，振子的位移x随时间t的变化如图所示，下列说法正确的是
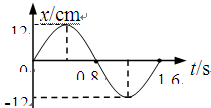
| A．t = 0.8s，振子的速度方向向左 |
| B．t = 0.2s时，振子在O点右侧6cm处 |
| C．t = 0.4s和t = 1.2s时，振子的加速度完全相同 |
| D．t=0.4s到t=0.8s的时间内，振子的速度逐渐减小 |
在光滑水平面上的O点系一长为l的绝缘细线，线的另一端系一质量为m，带电量为q的小球．当沿细线方向加—亡场强为E的匀强电场后，小球处于平衡状态．现给小球一垂直于细线的初速度v0，使小球在水平面上开始运动．若v0很小，则小球第一次回到平衡位置所需时间为__________.(见图)
一弹簧振子沿x轴振动，振幅为4cm，振子的平衡位置位于x轴上的O点，图中的a、b、c、d为四个不同的振动状态：黑点表示振子的位置，黑点上的箭头表示运动的方向．图中给出的①②③④四条振动图线，可用于表示振子的振动图象是 ( )
| A．若规定状态。时t=0，则图象为① |
| B．若规定状态^时t=0，则图象为② |
| C．若规定状态c时t=0，则图象为③ |
| D．若规定状态d时t=0，则图象为④ |
一个弹簧振子，第一次被压缩x后释放做自由振动，周期为T1，第二次被压缩2x后释放做自由振动，周期为T2，则两次振动周期之比T1∶T2为
| A．1∶1 | B．1∶2 | C．2∶1 | D．1∶4 |
某质点做简谐运动，其位移随时间变化的关系式为x＝Asin
，则质点 （ ）
| A．第1 s末与第3 s末的位移相同 |
| B．第1 s末与第3 s末的速度相同 |
| C．3 s末至5 s末的位移方向都相同 |
| D．3 s末至5 s末的速度方向都相同 |
如图所示,一简谐横波在x轴上传播,轴上a、b两点相距12 m.t=0时,a点为波峰,b点为波谷;t="0.5" s时,a点为波谷,b点为波峰.则下列判断中正确的是 ( )
| A．波长一定是24 m | B．波长可能是8 m |
| C．周期一定是1s | D．周期可能是 s |
粤公网安备 44130202000953号