如图所示，是一列沿x轴传播的简谐横波在t=0时刻的波形图，此时振动刚好传到x=2.0m处。已知波的传播速度为v=2m/s，则下列说法正确的是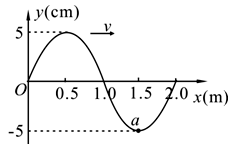
| A．x=0.5m处的质点的振动方程为y=5sin2πt（cm） |
| B．波传播到x=20m处时，质点起振方向沿y轴正方向 |
| C．此时图中质点a的加速度最小 |
| D．x=5.5m处的质点第一次到达波峰的时刻是2.5s |
如图所示，质量为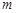
的物块放在弹簧上，与弹簧一起在竖直方向上做简谐运动，当振幅为A时，物体对弹簧的最大压力是物重的
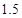倍，则物体对弹簧的最小压力是多少？要使物体在振动中不离开弹簧，振幅不能超过多大？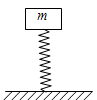
图l是一列简谐横波在t=1.25s时的波形图，已知c位置的质点比a位置的晚0.5s起振，则图2所示振动图象对应的质点可能位于（ ）
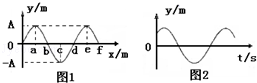
| A．a＜x＜b | B．b＜x＜c | C．c＜x＜d | D．d＜x＜e |
做简谐振动的单摆摆长不变，若摆球质量增加为原来的4倍，摆球经过平衡位置时速度减小为原来的1/2，则单摆振动的( )
| A．频率、振幅都不变 | B．频率、振幅都改变 |
| C．频率不变、振幅改变 | D．频率改变、振幅不变 |
如图甲所示,质量相等大小可忽略的a、b两小球用不可伸长的等长轻质细线悬挂起来,使小球a在竖直平面内来回摆动,小球b在水平面内做匀速圆周运动,连接小球b的绳子与竖直方向的夹角和小球a摆动时绳子偏离竖直方向的最大夹角都为θ,运动过程中两绳子拉力大小随时间变化的关系如图乙中c、d所示.则下列说法正确的是( )
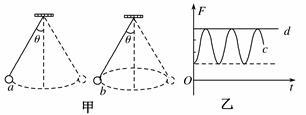
| A．图乙中直线d表示绳子对小球a的拉力大小随时间变化的关系 |
| B．图乙中曲线c表示绳子对小球a的拉力大小随时间变化的关系 |
| C．θ＝45° |
| D．θ＝60° |
下列有关简谐振动说法不正确的是（ ）
| A．做简谐振动的物体，受到的回复力的方向总是指向平衡位置 |
| B．平衡位置就是加速度为零的位置 |
| C．弹簧振子振动过程中动能和弹性势能相互转化，系统总机械能守恒 |
| D．弹簧振子振动过程中，弹性势能增加时，弹簧的长度可能变短 |
如图，t=0时刻，波源在坐标原点从平衡位置沿y轴正方向开始振动，振动周期为0.4s，在同一均匀介质中形成沿x轴正、负两方向传播的简谐横波。下图中能够正确表示t=0.6s时刻波形图的是
把一个筛子用四根弹簧支撑起来，筛子上装一个电动偏心轮，它每转一周，给筛子一个驱动力，这就做成了一个共振筛，如图甲所示。该共振筛的共振曲线如图乙所示。已知增大电压，可使偏心轮转速提高，增加筛子质量，可增大筛子的固有周期。现在，在某电压下电动偏心轮转速是54r/min．为了使筛子的振幅增大，下列做法正确的是
| A．提高输入电压 | B．降低输入电压 |
| C．减少筛子质量 | D．增加筛子质量 |
一列沿直线传播的简谐横波，其传播速度为80m/s，波源的振动图像如图所示，则这列波的波长和频率分别为
| A．800m，10Hz | B．8m，10Hz | C．8m，1Hz | D．4m，20Hz |
如下图所示，让摆球从图中的C位置由静止开始摆下，摆到最低点D处，摆线刚好被拉断，小球在粗糙的水平面上由D点向右做匀减速运动，到达小A孔进入半径R=0.3m的竖直放置的光滑圆弧轨道，当摆球进入圆轨道立即关闭A孔。已知摆线长L=2m，
，小球质量为m=1kg，D点与小孔A的水平距离s=2m，g取10m/s2。试求：
（1）求摆线能承受的最大拉力为多大？
（2）要使摆球能进入圆轨道并且不脱离轨道，求粗糙水平面摩擦因数μ的范围。
一个弹簧振子在光滑的水平面上作简谐运动，其中有两个时刻弹簧对振子的弹力大小相等，但方向相反，那么这两个时刻弹簧振子的（ ）
| A．速度一定大小相等，方向相反 |
| B．加速度一定大小相等，方向相反 |
| C．位移一定大小相等，方向相反 |
| D．以上三项都不一定大小相等，方向相反 |
竖直悬挂的弹簧振子下端装有记录笔，在竖直面内放置记录纸。当振子上下振动时，以水平向左速度v=10m/s匀速拉动记录纸，记录笔在纸上留下记录的痕迹，建立坐标系，测得的数据如图所示，求弹簧振子振动的振幅和频率。
一列简谐波沿x轴方向传播,已知x轴上x1=0和x2="1" m两处质点的振动图象分别如图(甲)、(乙)所示,
求(1)若此波沿x轴正向传播，则波的传播速度的可能值.
(2)若此波沿x轴负向传播，则波的传播速度的可能值.
粤公网安备 44130202000953号