如图,在竖直平面内由 圆弧 和 圆弧BC组成的光滑固定轨道,两者在最低点B平滑连接。 弧的半径为R, 弧的半径为 。一小球在A点正上方与A相距 处由静止开始自由下落,经A点沿圆弧轨道运动。
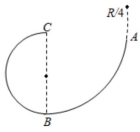
(1)求小球在B、A两点的动能之比;
(2)通过计算判断小球能否沿轨道运动到C点。
如图,一固定容器的内壁是半径为R的半球面;在半球面水平直径的一端有一质量为m的质点P。它在容器内壁由静止下滑到最低点的过程中,克服摩擦力做的功为W。重力加速度大小为g。设质点P在最低点时,向心加速度的大小为a,容器对它的支持力大小为N,则 ( )
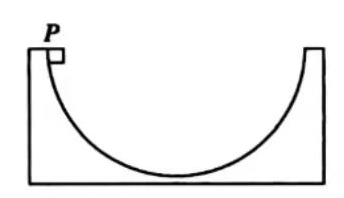
| A. |
|
B. |
|
C. |
|
D. |
|
在星球
上将一轻弹簧竖直固定在水平桌面上,把物体P轻放在弹簧上端,P由静止向下运动,物体的加速度a与弹簧的压缩量x间的关系如图中实线所示。在另一星球N上用完全相同的弹簧,改用物体Q完成同样的过程,其
关系如图中虚线所示,假设两星球均为质量均匀分布的球体。已知星球M的半径是星球N的3倍,则( )

A.M与N的密度相等
B.Q的质量是P的3倍
C.Q下落过程中的最大动能是P的4倍
D.Q下落过程中弹簧的最大压缩量是P的4倍
如图,在摩托车越野赛途中的水平路段前方有一个坑,该坑沿摩托车前进方向的水平宽度为 ,其左边缘 点比右边缘 点高 。若摩托车经过 点时的动能为 ,它会落到坑内 点, 与 的水平距离和高度差均为 ;若经过 点时的动能为 ,该摩托车恰能越过坑到达 点。 等于

| A. |
20 |
B. |
18 |
C. |
9.0 |
D. |
3.0 |
一篮球质量为 ,一运动员使其从距地面高度为 处由静止自由落下,反弹高度为 。若使篮球从距地面 的高度由静止下落,并在开始下落的同时向下拍球,球落地后反弹的高度也为 。假设运动员拍球时对球的作用力为恒力,作用时间为 ;该篮球每次与地面碰撞前后的动能的比值不变。重力加速度大小取 ,不计空气阻力。求:
(1)运动员拍球过程中对篮球所做的功;
(2)运动员拍球时对篮球的作用力的大小。
水平桌面上,一质量为m的物体在水平恒力F拉动下从静止开始运动。物体通过的路程等于 时,速度的大小为 ,此时撤去F,物体继续滑行 的路程后停止运动。重力加速度大小为g。则( )
| A. |
在此过程中F所做的功为 |
| B. |
在此过程中F的冲量大小等于 |
| C. |
物体与桌面间的动摩擦因数等于 |
| D. |
F的大小等于物体所受滑动摩擦力大小的2倍 |
如图,相距 的两平台位于同一水平面内,二者之间用传送带相接。传送带向右匀速运动,其速度的大小 可以由驱动系统根据需要设定。质量 的载物箱(可视为质点),以初速度 自左侧平台滑上传送带。载物箱与传送带间的动摩擦因数 ,重力加速度取 。
(1)若 ,求载物箱通过传送带所需的时间;
(2)求载物箱到达右侧平台时所能达到的最大速度和最小速度;
(3)若 ,载物箱滑上传送带△ 后,传送带速度突然变为零。求载物箱从左侧平台向右侧平台运动的过程中,传送带对它的冲量。

如图所示,小球 、 分别从 和 的高度水平抛出后落地,上述过程中 、 的水平位移分别为 和 。忽略空气阻力,则

| A. |
和 的位移大小相等 |
B. |
的运动时间是 的2倍 |
| C. |
的初速度是 的 |
D. |
的末速度比 的大 |