高中物理动量定理试题

下面的说法正确的是（   ）

A．物体运动的方向就是它的动量的方向

B．如果物体的速度发生变化，则可以肯定它受到的合外力的冲量不为零

C．如果合外力对物体的冲量不为零，则合外力一定使物体的动能增大

D．作用在物体上的合外力冲量不一定能改变物体速度的大小

(9分）如图所示，光滑水平面上一质量为M、长为L的木板右端靠竖直墙壁。质量为m的小滑块（可视为质点）以水平速度v₀滑上木板的左端，滑到木板的右端时速度恰好为零。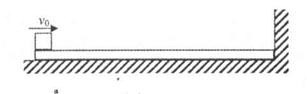

①求小滑块与木板间的摩擦力大小；
②现小滑块以某一速度v滑上木板的左端，滑到木板的右端时与竖直墙壁发生弹性碰撞，然后向左运动，刚好能够滑到木板左端而不从木板上落下，试求的值。

如图所示，静置于水平地面的三辆手推车沿一直线排列，质量均为m，人在极端的时间内给第一辆车一水平冲量使其运动，当车运动了距离L时与第二辆车相碰，两车以共同速度继续运动了距离L时与第三车相碰，三车以共同速度又运动了距离L时停止。车运动时受到的摩擦阻力恒为车所受重力的k倍，重力加速度为g,若车与车之间仅在碰撞时发生相互作用，碰撞时间很短，忽略空气阻力，求：

(1)整个过程中摩擦阻力 所做的总功；
(2)人给第一辆车水平冲量的大小；
(3)第一次与第二次碰撞系统功能损失之比。

如图所示，斜面上除AB段粗糙外，其余部分均是光滑的，且物体与AB段动摩擦系数处处相同。今使物体（视为质点）由斜面顶端O处由静止开始下滑，经过A点时的速度与经过C点时的速度相等。AB=BC，则下列判断正确的是（     ）

A．物体在AB段与BC段的加速度相等

B．物体在AB段与BC段的运动时间相等

C．重力在这两段中所做功相等

D．物体在AB段与BC段动量变化量相同

如图所示，质量为m的小物块以水平速度v₀滑上原来静止在光滑水平面上质量为M的小车上，物块与小车间的动摩擦因数为μ，小车足够长。求：

①小物块相对小车静止时的速度；
②从小物块滑上小车到相对小车静止所经历的时间；
③从小物块滑上小车到相对小车静止时，物块相对小车滑行的距离。

在空中某处以速度v₀水平抛出一质量为m的物体，经过时间t，当物体下落高度h后，其速度大小仍为v₀，但方向与初速度方向相反，如图所示。下列说法错误的是（    ）

A．物体机械能减少mgh	B．物体机械能减少mg^2t^2
C．风力对物体做功为零	D．风力对物体做负功，其数值等于物体机械能的变化

人从高处跳到低处时，为了安全，一般都让脚尖着地后膝盖弯曲，这样做是为了

A．减小冲量

B．减小动量的变化量

C．增大与地面的作用时间，从而减小冲力

D．增大人对地面的压强，起到安全作用

如图所示，m_A=1kg，m_B=4kg，小物块m_C=1kg，ab、dc段均光滑，且dc段足够长；物体A、B上表面粗糙，最初均处于静止．小物块C静止在a点，已知ab长度L=16m，现给小物块C一个水平向右的瞬间冲量I₀=6N•s.

(1)当C滑上A后，若刚好在A的右边缘与A具有共同的速度v₁(此时还未与B相碰)，求v₁的大小．
(2)A、C共同运动一段时间后与B相碰，若已知碰后A被反弹回来，速度大小为0.2m/s，C最后和B保持相对静止，求B、C最终具有的共同速度v₂.

一倾角为的斜面固定于地面，斜面顶端离地面的高度h₀=1m，斜面底端有一垂直于斜面的固定挡板。在斜面顶端自由释放一质量m=0.09kg的小物块（视为质点）。小物块与斜面之间的动摩擦因数u=0.2。当小物块与挡板碰撞后，将以原速返回。重力加速度g="10" m/s²。在小物块与挡板的前4次碰撞过程中，挡板给予小物块的总冲量是多少？

(16分) 质量为1 kg的物体从离地面5 m高处自由下落，与地面碰撞后，上升的最大高度为3.2 m，设球与地面作用时间为0.2 s，求小球对地面的平均作用力．（g =" 10" m/s²，不计空气阻力）

试用牛顿运动定律推导动量守恒定律

如图所示，在光滑水平地面上有一固定的挡板，挡板上固定一个轻弹簧。现有一质量，长的小车（其中为小车的中点，部分粗糙，部分光滑），一质量为的小物块（可视为质点），放在车的最左端，车和小物块一起以的速度在水平面上向右匀速运动，车撞到挡板后瞬间速度变为零，但未与挡板粘连。已知车部分的长度大于弹簧的自然长度，弹簧始终处于弹性限度内，小物块与车部分之间的动摩擦因数为0.3，重力加速度。求：

（1）小物块和弹簧相互作用的过程中，弹簧具有的最大弹性势能；
（2）小物块和弹簧相互作用的过程中，弹簧对小物块的冲量；
（3）小物块最终停在小车上的位置距端多远。

如图所示，质量m_A="2" kg木块A静止在光滑水平面上。一质量m_B=" 1" kg的木块B以某一初速度v₀="5" m/s向右运动，与A碰撞后均向右运动。木块A 向右运动，与挡板碰撞反弹（与挡板碰撞无机械能损失)。后来与B发生二次碰撞，碰后A、B同向运动，速度分别为0.9 m/s、1.2 m/s。求：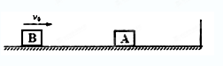

（1）第一次A、B碰撞后A的速度；
（2）第二次碰撞过程中，A对B做的功。

2014年8月3日我国云南鲁甸发生里氏6.5级地震，为救援灾区人民，要从悬停在空中的直升机上投放救灾物资，每箱救灾物资的质量为20 kg，设箱子承受的地面冲击力大小为1 000 N，箱子与地面的作用时间为0.5 s，已知当地的重力加速度g＝10 m/s²，不计空气阻力，试求：
(1)与地面作用时，箱子的加速度是多少？
(2)为保证救灾物资安全落地，飞机投放物资时的高度不应超过多少米？

如图所示，光滑水平面上一质量为M、长为L的木板右端靠竖直墙壁。质量为m 的小滑块（可视为质点）以水平速度滑上木板的左端，滑到木板的右端时速度恰好为零。

①求小滑块与木板间的摩擦力大小；
②现小滑块以某一速度滑上木板的左端，滑到木板的右端时与竖直墙壁发生弹性碰 撞，然后向左运动，刚好能够滑到时木板左端而不从木板上落下，试求的值。