高中物理同步卫星计算题

如图所示，P是一颗地球同步卫星，已知球半径为R，地球表面处的重力加速度为R，地球自转周期为T。

（1）设地球同步卫星对地球的张为2θ，求同步卫星的轨道半径r和sinθ的值。
（2）要使一颗地球同步卫星能覆盖赤道上，A，B之间的区域，∠AOB=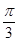，则卫星可定位在轨道某段圆弧上，求该段圆弧的长度l（用r和θ表示）

我国自主研制的北斗卫星导航系统包括5颗静止轨道卫星（同步卫星）和30颗非静止轨道卫星，将为全球用户提供高精度、高可靠性的定位、导航服务。
A为地球同步卫星，质量为m₁；B为绕地球做圆周运动的非静止轨道卫星，质量为m₂，离地面高度为h.已知地球半径为R，地球自转周期为T₀，地球表面的重力加速度为g。 求：
(1)卫星A运行的角速度；(2)卫星B运行的线速度。

我国自主研制的北斗卫星导航系统包括5颗静止轨道卫星（同步卫星）和30颗非静止轨道卫星，将为全球用户提供高精度、高可靠性的定位、导航服务。
A为地球同步卫星，质量为m₁；B为绕地球做圆周运动的非静止轨道卫星，质量为m₂，离地面高度为h.已知地球半径为R，地球自转周期为T₀，地球表面的重力加速度为g。 求：
(1)卫星A运行的角速度；(2)卫星B运行的线速度。

月球绕地球运动的轨道半径约为地球半径的60倍，运行周期约为27天，（地球半径R_地=6.4×10³km，万有引力恒量为G。)，（计算结果可以保留根号，且只要数量级对就给满分）
求：（1）地球同步卫星离地面的高度约为多少千米？
（2）地球的质量约为多少？
（3）月球绕地球运动的线速度约为多少？

(15分)如图所示，A是地球的同步卫星，另一卫星B的圆形轨道位于赤道平面内，离地球表面的高度为h，已知地球半径为R，地球自转角速度为ω₀，地球表面的重力加速度为g，O为地球中心．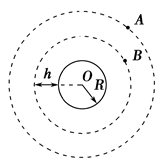

(1)求卫星B的运行周期．
(2)如果卫星B绕行方向与地球自转方向相同，某时刻A、B两卫星相距最近(O、A、B在同一直线上)，则至少经过多长时间，它们再一次相距最近？

天文学家将相距较近、仅在彼此的引力作用下运行的两颗恒星称为双星。双星系统在银河系中很普遍。经观测某双星系统中两颗恒星A、B围绕它们连线上的某一固定点分别做匀速圆周运动，周期均为T 。已知恒星A、B之间的距离为L，A、B的质量之比2 ：1，万有引力常量为G，求：
（1）恒星A做匀速圆周运动的轨道半径R_A；
（2）双星的总质量M 。

(8 分）.已知地球同步卫星离地面的高度约为地球半径的6倍。若某行星的平均密度为地球平均密度的一半，它的同步卫星距其表面的高度是其半径的2.5倍，求：该行星的自转周期。

利用水流和太阳能发电，可以为人类提供清洁能源。水的密度ρ=1×10³kg/m³，太阳光垂直照射到地面上时的辐射功率P₀ =1×10³W/m²，地球半径为R=6.4×10⁶m，地球表面的重力加速度取g=10m/s²。
⑴写出太阳光照射到地球表面的总功率P的字母表达式；
⑵发射一颗卫星到地球同步轨道上（轨道半径约为地球半径的6.6≈倍）利用太阳能发电，然后通过微波持续不断地将电力输送到地面，这样就建成了太阳能发电站。求卫星在地球同步轨道上向心加速度的大小（答案保留两位有效数字）；
⑶三峡水电站水库面积约为S=1×10⁹m²，平均流量Q=1.5×10⁴m³/s，水库水面与发电机所在位置的平均高度差为h=100m，发电站将水的势能转化为电能的总效率η₁=60%。在地球同步轨道上，太阳光垂直照射时的辐射功率为1.4P₀。太阳能电池板将太阳能转化为电能的效率为η₂=20％，将电能输送到地面的过程要损失50%。若要使⑵中的太阳能发电站在被太阳照射时地面接收到的电功率相当于三峡电站发电的平均功率，卫星上太阳能电池板的面积应为多大？(保留一位有效数字)

如图所示，A是地球的同步卫星，另一卫星B的圆形轨道位于赤道平面内，离地面高度为h.已知地球半径为R，地球自转角速度为ω₀，地球表面的重力加速度为g，O为地球中心．

(1)求卫星B的运行周期．
(2)如卫星B绕行方向与地球自转方向相同，某时刻A、B两卫星相距最近(O、B、A在同一直线上)，则至少经过多长时间，他们再一次相距最近？

如图所示，设A、B为地球赤道圆的一条直径的两端，利用地球同步卫星将一电磁波信号由A传播到B，至少需要几颗同步卫星？这几颗同步卫星间的最近距离是多少？用这几颗同步卫星把电磁波信号由A传播到B需要的时间是多少？（已知地球半径R，地表面处的重力加速度g，地球自转周期T，不考虑大气层对电磁波的影响且电磁波在空气中的传播速度为c）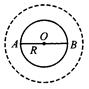

(1)已知地球质量为M,引力常量为G,地球自转周期为T.求同步卫星离地心的距离.
(2)已知地球半径为R, 地球自转周期为T,贴近地球运行的卫星的周期为T₀.求同步卫星离地心的距离.
(3)已知地球半径为R,地面附近引力场强度约等于地面附近重力加速度g,地球自转周期为T.求同步卫星离地心的距离.

发射地球同步卫星时，先将卫星发射至距地面高度为h₁的近地轨道上，在卫星经过A点时点火，实施变轨，进入远地点为B的椭圆轨道上，最后在B点再次点火，将卫星送入同步轨道，如图所示．已知同步卫星的运动周期为T，地球的半径为R，地球表面重力加速度为g，求：

（1）卫星在近地点A的加速度大小；
（2）远地点B距地面的高度

已知地球质量为M，半径为R，自转周期为T，引力常量为G。如图所示，A为在地面附近绕地球做匀速圆周运动的卫星，B为地球的同步卫星。

（1）求卫星A运动的速度大小v；
（2）求卫星B到地面的高度h。

知万有引力常量C，地球半径R，月球和地球之间的距离r，同步卫星距地面的高度h，月球绕地球的运转周期T_l，地球的自转周期T₂，地球表面的重力加速度g．某同学根据以上条件，提出一种估算地球质量"的方法：
同步卫星绕地心做圆周运动，由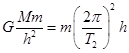 得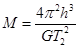
(1)请判断上面的结果是否正确，并说明理由．如不正确，请给出正确的解法和结果
(2)请根据已知条件再提出两种估算地球质量的方法并解得结果

已知地球半径为R，地球同步卫星离地面的高度为h，周期为T₀。另有一颗轨道平面在赤道平面内绕地球自西向东运行的卫星，某时刻该卫星能观察到的赤道弧长最大为赤道周长的三分之一。求（1）该卫星的周期；（2）该卫星相邻两次经过地球赤道上某点的上空所需的时间。