高中物理人造卫星计算题

“嫦娥一号”的成功发射，为实现中华民族几千年的奔月梦想迈出了重要的一步.如图所示，“嫦娥一号”先进入绕月飞行的椭圆轨道，然后再椭圆轨道近月点变轨进入绕月飞行圆轨道；已知“嫦娥一号”绕月飞行的椭圆轨道远月点距月球表面高度为；又已知“嫦娥一号”绕月圆轨道飞行时，距月球表面的高度为，飞行周期为，月球的半径为，万有引力常量为；再后，假设宇航長在飞船上，操控飞船在月球表面附近竖直平面内俯冲，在最低点附近作半径为的圆周运动，宇航员质量是，飞船经过最低点时的速度是．求：

（1）月球的质量是多大？
（2）“嫦娥一号”经绕月飞行的椭圆轨道远月点时的加速度多大？“嫦娥一号”经绕月飞行的椭圆轨道近月点时欲变轨进入如图圆轨道，应该向前还是向后喷气？
（3）操控飞船在月球表面附近竖直平面内俯冲经过最低点时，座位对宇航员的作用力是多大？

2013年6月，我国成功实现目标飞行器“神舟十号”与轨道空间站“天宫一号”的对接．如图所示，已知“神舟十号”从捕获“天宫一号”到实现对接用时t，这段时间内组合体绕地球转过的角度为θ（此过程轨道不变，速度大小不变），地球半径为R，地球表面重力加速度为g，万有引力恒量G，不考虑地球自转；求：（1）地球质量M；（2）组合体运动的周期T；（3）组合体所在圆轨道离地高度H。

我国在2007年成功发射一颗绕月球飞行的卫星，计划在2012年前后发射一颗月球软着陆器，在2017年前后发射一颗返回式月球软着陆器，进行首次月球样品自动取样并安全返回地球．设想着陆器完成了对月球表面的考察任务后，由月球表面回到围绕月球做圆周运动的轨道舱，其过程如图3－4－7所示．设轨道舱的质量为m，月球表面的重力加速度为g，月球的半径为R，轨道舱到月球中心的距离为r，引力常量为G，则试求：

(1)月球的质量；
(2)轨道舱的速度大小和周期．

地球的两颗人造卫星质量之比m₁∶m₂＝1∶2，轨道半径之比r₁∶r₂＝1∶2.求：
(1)线速度大小之比．
(2)角速度之比．
(3)运行周期之比．
(4)向心力大小之比．

我国执行首次载人航天飞行的神州五号飞船于2003年10月15日在中国酒泉卫星发射中心发射升空．飞船由长征-2F运载火箭先送入近地点为A、远地点为B的椭圆轨道，在B点实施变轨后，再进入预定圆轨道，如图所示。已知飞船在预定圆轨道上飞行n圈所用时间为t，近地点A距地面高度为h₁，地球表面重力加速度为g，地球半径为R，求：

（1）地球的第一宇宙速度大小；
（2）飞船在近地点A的加速度a_A大小；
（3）远地点B距地面的高度h₂大小。

“嫦娥二号”卫星是在绕月极地轨道上运动的，加上月球的自转，卫星能探测到整个月球的表面。如图所示，卫星上CD相机已对月球背面进行成像探测，并获取了月球背面部分区域的影像图。卫星在绕月极地轨道上做圆周运动时距月球表面高为H，绕行的周期为T_M；月球绕地公转的周期为T_E，半径为R₀。地球半径为R_E，月球半径为R_M。试解答下列问题：

（1）若忽略地球及太阳引力对绕月卫星的影响，试求月球与地球质量之比；
（2）当绕月极地轨道的平面与月球绕地公转的轨道平面垂直，也与地心到月心的连线垂直。此时探月卫星向地球发送所拍摄的照片，此照片由探月卫星传送到地球最少需要多长时间？已知光速为C。

两颗卫星在同一轨道平面内绕地球做绕向相同的匀速圆周运动，设地球平均半径为R，a卫星离地面高为R，b卫星离地面高为3R，若某时该两卫星正好同时通过地面同一点正上方，试求从两卫星位于地面同一点正上方开始，两卫星第一次出现最远距离的时间是a卫星周期的几倍？

高空遥感探测卫星在距地球表面高为2R处绕地球转动。人造卫星质量为m，地球半径为R，地球表面重力加速度为g，
试求：（1）人造卫星的运行速度大小v；
（2）人造卫星绕地球转动的周期T；
（3）人造卫星的向心加速度a_n。

2014年10月8日，月全食带来的“红月亮”亮相天空，引起人们对月球的关注。我国发射的“嫦娥三号”探月卫星在环月圆轨道绕行n圈所用时间为t，如图所示。已知月球半径为R，月球表面处重力加速度为g_月，引力常量为G．试求：

（1）月球的质量M；
（2）月球的第一宇宙速度v₁；
（3）“嫦娥三号”卫星离月球表面高度h．

“神舟十号”宇宙飞船成功发射，表明了我国的航天和空间科技已经进人世界先进行列。它的部分数据如下：总质量为m，绕地球做匀速圆周运动的周期为T。若已知地球半径R，地球表面的重力加速度为g，万有引力常量为G，请你根据以上的已知量，用所学过的物理知识，求：
（1）地球的平均密度ρ.
（2）飞船距离地球表面的高度h.

已知“天宫一号”在地球上空的圆轨道上运行时离地面的高度为h。地球半径为R，地球表面的重力加速度为g，万有引力常量为G。求：
（1）地球的密度为多少？   
（2）“天宫一号”在该圆轨道上运行时速度v的大小；

(15分)如图所示，A是地球的同步卫星，另一卫星B的圆形轨道位于赤道平面内，离地球表面的高度为h，已知地球半径为R，地球自转角速度为ω₀，地球表面的重力加速度为g，O为地球中心．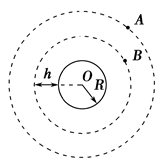

(1)求卫星B的运行周期．
(2)如果卫星B绕行方向与地球自转方向相同，某时刻A、B两卫星相距最近(O、A、B在同一直线上)，则至少经过多长时间，它们再一次相距最近？

“嫦娥三号”探测器于2013年12月2日凌晨在西昌发射中心发射成功。“嫦娥三号”经过几次成功变轨以后，探测器状态极其良好，成功进入绕月轨道。12月14日21时11分，“嫦娥三号”探测器在月球表面预选着陆区域成功着陆，标志我国已成为世界上第三个实现地外天体软着陆的国家。 设“嫦娥三号”探测器环绕月球的运动为匀速圆周运动,它距月球表面的高度为h,已知月球表面的重力加速度为g、月球半径为R,引力常量为G,则
（1）探测器绕月球运动的向心加速度为多大；
（2）探测器绕月球运动的周期为多大。

“神州”六号飞船发射成功后，进入圆形轨道稳定运行，运转一周的时间为T，地球的半径为R，表面重力加速度为g，万有引力常量为G，试求：
（1）地球的密度；
（2）“神州”六号飞船轨道距离地面的高度。

高空遥感探测卫星在距地球表面高为h处绕地球转动，如果地球质量为M，地球半径为R，人造卫星质量为m，万有引力常量为G，求：
（1）人造卫星的角速度多大？
（2）人造卫星绕地球转动的周期是多少？
（3）人造卫星的向心加速度多大？