开普勒三定律也适用于神舟七号飞船的变轨运动. 飞船与火箭分离后进入预定轨道, 飞船在近地点(可认为近地面)开动发动机加速, 之后,飞船速度增大并转移到与地球表面相切的椭圆轨道, 飞船在远地点再次点火加速, 飞船沿半径为r的圆轨道绕地运动. 设地球半径为R,地球表面的重力加速度为g,若不计空气阻力,试求神舟七号从近地点到远地点时间(变轨时间).
神奇的黑洞是近代引力理论所预言的一种特殊天体,探寻黑洞的方案之一是观测双星系统的运动规律.天文学家观测河外星系大麦哲伦云时,发现了LMCX-3双星系统,它由可见星A和不可见的暗星B构成.两星视为质点,不考虑其它星体的影响,A、B围绕两者连线上的O点做匀速圆周运动,它们之间的距离保持不变,如图18所示.引力常量为G,由观测能够得到可见星A的速率v和运行周期T.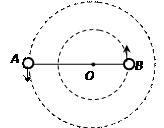
可见星A所受暗星B的引力FA可等效为位于O点处质量为
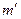 的星体(可视为质点)对它的引力,设A和B的质量分别为m1、m2,试求
的星体(可视为质点)对它的引力,设A和B的质量分别为m1、m2,试求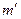 (用m1、m2表示);
(用m1、m2表示);求暗星B的的质量m2与可见星A的速率v、运行周期T和质量m1之间的关系式;
恒星演化到末期,如果其质量大于太阳质量ms的2倍,它将有可能成为黑洞.若可见星A的速率
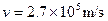 ,运行周期
,运行周期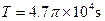 ,质量m1=6ms,试通过估算来判断暗星B有可能是黑洞吗? 图18
,质量m1=6ms,试通过估算来判断暗星B有可能是黑洞吗? 图18
( ,
,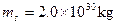 )
)
假设太阳系中天体的密度不变,天体直径和天体之间距离都缩小到原来的一半,地球绕太阳公转近似为匀速圆周运动,则下列物理量变化正确的是()
| A. | 地球的向心力变为缩小前的一半 |
| B. |
地球的向心力变为缩小前的
|
| C. | 地球绕太阳公转周期与缩小前的相同 |
| D. | 地球绕太阳公转周期变为缩小前的一半 |
在地球某处海平面上测得物体自由下落高度h所需的时间为t,到某高山顶测得物体自由下落h同样高度所需时间增加了Δt,已知地球半径为,试求山的高度H.
目前,在地球周围有许多人造地球卫星绕着它转,其中一些卫星的轨道可近似为圆,且轨道半径逐渐变小。若卫星在轨道半径逐渐变小的过程中,只受到地球引力和稀薄气体阻力的作用,则下列判断正确的是( )
| A.卫星的动能逐渐减小 |
| B.由于地球引力做正功,引力势能一定减小 |
| C.由于气体阻力做负功,地球引力做正功,机械能保持不变 |
| D.卫星克服气体阻力做的功小于引力势能的减小 |
“嫦娥一号”卫星开始绕地球在椭圆轨道运动,经过变轨、制动后,成为一颗绕月球做圆周运动的卫星。设卫星距月球表面的高度为h ,做匀速圆周运动的周期为T 。已知月球半径为R ,引力常量为G。求:
(1)月球的质量M及月球表面的重力加速度g;
(2)在距月球表面高度为h0的地方(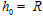 ),将一质量为m的小球以v0的初速度水平抛出,求落地瞬间月球引力对小球做功的瞬时功率P。
),将一质量为m的小球以v0的初速度水平抛出,求落地瞬间月球引力对小球做功的瞬时功率P。
《科学》介绍了一种新技术——航天飞缆,航天飞缆是用柔性缆索将两个物体连接起来在太空飞行的系统。飞缆系统在太空飞行中能为自身提供电能和拖曳力,它还能清理“太空垃圾”等。该系统的工作原理可用物理学的基本定律来解释。
下图为飞缆系统的简化模型示意图,图中两个物体P,Q的质量分别为mP、mQ,柔性金属缆索长为l,外有绝缘层,系统在近地轨道作圆周运动,运动过程中Q距地面高为h。设缆索总保持指向地心,P的速度为vP。已知地球半径为R,地面的重力加速度为g。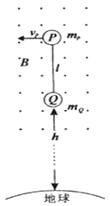
(1)飞缆系统在地磁场中运动,地磁场在缆索所在处的磁感应强度大小为B,方向垂直于纸面向外。设缆索中无电流,求缆索P、Q哪端电势高?两端的电势差多大?
(2)设缆索的电阻为R1,如果缆索两端物体P、Q通过周围的电离层放电形成电流,相应的电阻为R2,求缆索所受的安培力多大?
(3)求缆索对Q的拉力FQ多大?
嫦娥二号卫星由地面发射后,进入地月转移轨道,经多次变轨最终进入距离月球表面100公里,周期为118分钟的工作轨道,开始对月球进行探测,则下列说法错误的是( )
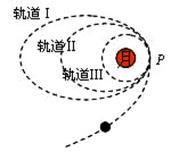
| A.卫星在轨道Ⅲ上的运动速度比月球的第一宇宙速度小 |
| B.卫星在轨道Ⅲ上运动周期比在轨道Ⅰ上小 |
| C.卫星在轨道Ⅲ上经过P点的速度比在轨道Ⅰ上经过P点时大 |
| D.卫星在轨道Ⅰ上经过P点的加速度等于在轨道Ⅱ上经过P点的加速度 |
今年7月23日凌晨,美国宇航局(NASA)发布消息称其天文学家们发现了迄今“最接近另一个地球”的系外行星,因为围绕恒星Kepler 452运行,这颗系外行星编号为Kepler 452b,其直径约为地球的1.6倍,与恒星之间的距离与日地距离相近,其表面可能存在液态水,适合人类生存。设Kepler 452b在绕恒星Kepler 452圆形轨道运行周期为T1,神舟飞船在地球表面附近圆形轨道运行周期为T2,恒星Kepler 452质量与地球质量之比为p,Kepler 452b绕恒星Kepler 452的轨道半径与地球半径之比为q,则T1、T2之比为
A.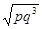 B.
B.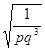 C.
C.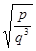 D.
D.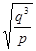
“神舟八号”与“天宫一号”对接前各自绕地球运动,设“天宫一号”在半径为r1的圆轨道上运动,周期为T1,“神舟八号”在半径为r2的圆轨道上运动,r1>r2,则
| A.“天宫一号”的运行速度大于7.9 km/s |
B.“神舟八号”的周期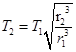 |
C.地球表面的重力加速度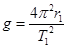 |
D.地球的质量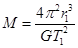 |
人造卫星绕地球只受地球的引力,做匀速圆周运动,其轨道半径为r,线速度为v,周期为T。为使其周期变为8T,可采用的方法有
| A.保持轨道半径不变,使线速度减小为v/8 |
| B.逐渐减小卫星质量,使轨道半径逐渐增大为4r |
| C.逐渐增大卫星质量,使轨道半径逐渐增大为8r |
| D.保持线速度不变v,将轨道半径增加到8r |
如图所示,太阳和地球组成“日地双星系统”,两者绕共同的圆心 点(图中未画出)做周期相同的圆周运动.数学家拉格朗日发现,处在拉格朗日点(如图所示)的航天器在太阳和地球引力的共同作用下可以绕“日地双星系统”的圆心
点(图中未画出)做周期相同的圆周运动.数学家拉格朗日发现,处在拉格朗日点(如图所示)的航天器在太阳和地球引力的共同作用下可以绕“日地双星系统”的圆心 点做周期相同的圆周运动,从而使日、地、航天器三者在太空的相对位置保持不变.不考虑航天器对日地双星系统的影响,不考虑其它天体对该系统的影响.已知:太阳质量为
点做周期相同的圆周运动,从而使日、地、航天器三者在太空的相对位置保持不变.不考虑航天器对日地双星系统的影响,不考虑其它天体对该系统的影响.已知:太阳质量为 ,地球质量为
,地球质量为 ,太阳与地球球心距离为
,太阳与地球球心距离为 .则下列说法正确的是
.则下列说法正确的是
A.位于拉格朗日点的绕 点稳定运行的航天器,其向心加速度小于地球的向心加速度 点稳定运行的航天器,其向心加速度小于地球的向心加速度 |
B.日地双星系统的周期为 |
C.圆心 点在太阳和地球的连线上,距离太阳和地球球心的距离之比等于太阳和地球的质量之比 点在太阳和地球的连线上,距离太阳和地球球心的距离之比等于太阳和地球的质量之比 |
D.拉格朗日点距地球球心的距离 满足关系式 满足关系式 |
在半径R=5 000 km的某星球表面,宇航员做了如下实验,实验装置如图甲所示.竖直平面内的光滑轨道由轨道AB和圆弧轨道BC组成,将质量m=0.2 kg的小球,从轨道AB上高H处的某点由静止滑下,用力传感器测出小球经过C点时对轨道的压力F,改变H的大小,可测出相应的F大小,F随H的变化关系如图乙所示.求:
(1)圆轨道的半径及星球表面的重力加速度.
(2)该星球的第一宇宙速度.
假设有一载人宇宙飞船在距地面高度为4200km 的赤道上空绕地球做匀速圆周运动,地球半径约为6400km,地球同步卫星距地面高度为36000km,宇宙飞船和地球同步卫星绕地球同向运动,每当二者相距最近时,宇宙飞船就向同步卫星发射信号,然后再由同步卫星将信号发送到地面接收站,某时刻二者相距最远,从此刻开始,在一昼夜的时间内,接收站共接收到信号的次数为 ( )
| A.4次 | B.6次 | C.7次 | D.8次 |