高中物理万有引力定律及其应用综合题

神舟六号飞船2005年10月12日9时在酒泉发射场升空，在太空环绕地球五天后，按预定的程序平稳地在内蒙古中部着陆。若将飞船环绕地球的运动看作匀速圆周运动时距地面的高度为h，绕地球一周的时间为T，地球半径为R。引力常量为G。
求
（1）飞船在环绕地球做圆周运动的加速度大小
（2）地球的质量

已知地球自转周期T,地球半径为R，地球表面重力加速度为g,请使用上述已知量导出地球同步卫星距离地面的高度h的表达式，并说明同步卫星的轨道特点，运转方向。

(1)火星的第一宇宙速度是多少？
(2)火星表面附近的重力加速度g是多少？
(3)若你的质量是m、秋千的绳长l、绳与竖直方向的最大夹角等于θ，求你经过最低点的速度大小？

（1）该位置处的重力加速度g′是地面处重加速度g的多少倍？
（2）该位置距地球表面的高度h为多大？

（2）“神舟六号”进入圆形轨道运动后，其绕地球运行的周期T为多少？（地球半径为km，地球表面附近重力加速度g=10m/s²,结果保留一位有效数字）

地球质量为M，半径为R，万有引力恒量为G。若已知第一宇宙速度=7．9k／s，地球半径R=6．4×10³km，万有引力恒量G=6．67×10N·m²·kg。
求：（1）第一宇宙速度的计算式；
（2）地球的质量（要求保留两位有效数字）。

⑴有一颗近地卫星绕地球表面运动，试估算其运行周期T的平方?
⑵试用地球的平均半径R、地球表面的重力加速度g、引力常量G导出地球的平均密度的表达式．

中子星是恒星演化过程的一种可能结果，它的密度很大。现有一中子星，观测到它的自转周期为T=s。问该中子星的最小密度应是多少才能维持该星的稳定，不致因自转而瓦解。计算时星体可视为均匀球体。(引力常数G=6.6710m/kg·s)

对某行星的一颗卫星进行观测，已知运行的轨迹是半径为r的圆周，周期为T，求：
（1）该行星的质量；
（2）测得行星的半径为卫星轨道半径的1/10，则此行星表面重力加速度为多大？

（1）已知地球半径为R，地球表面重力加速度为g，地球自转周期为T₀，请用以上物理量表示“风云二号”D气象卫星的轨道半径r，加速度a 以及线速度v ；
（2）取R=6400km，g=10m/s²，π²=10，，求出“风云二号”D气象卫星的轨道半径r；
（3）根据第（2）问的结果，定性说明“风云二号”D气象卫星的加速度与随地球一块转动的赤道上物体的加速度的大小关系。

1789年英国著名物理学家卡文迪许首先估算出了地球的平均密度。根据你学过的知识，能否知道地球平均密度的大小。

猜想、检验是科学探究的两个重要环节．月－地检验为万有引力定律的发现提供了事实依据．请你完成如下探究内容：（1）已知地球中心与月球的距离r=60R (R为地球半径，R=6400km)，计算月球由于受到地球的万有引力而产生的加速度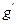；（2）已知月球绕地球运转的周期为27.3天，地球中心与月球的距离r=60R，计算月球绕地球运动的向心加速度．

如图所示，在距一质量为M、半径为R、密度均匀的球体中心2R处，有一质量为m的质点，M对m的万有引力的大小为F。现从M中挖出一半径为r的球体，如图，OO′=R/2。求M中剩下的部分对m的万有引力的大小。