高中物理万有引力定律及其应用填空题

两颗人造卫星A、B的质量之比m_A∶m_B=1∶2，轨道半径之比r_A∶r_B=1∶3，某一时刻它们的连线通过地心，则此时它们的线速度之比v_A∶v_B=        ，向心加速度之比a_A∶a_B=      ，向心力之比F_A∶F_B=          。

地核的体积约为整个地球体积的16%，地核的质量约为地球质量的34%.经估算，地核的平均密度为_______kg/m³.（已知地球半径为6.4×10⁶ m，地球表面重力加速度为9.8 m/s²，万有引力常量为6.7×10^－11N·m²/kg²，结果取两位有效数字。）

宇宙中存在一些离其它恒星较远的、由质量相等的三颗星组成的三星系统（假设三颗星的质量均为m，引力常量为G），通常可忽略其它星体对它们的引力作用。已观测到稳定的三星系统存在两种基本的构成形式：第一种形式是三颗星位于同一直线上，两颗星围绕中央星在同一半径为R的圆轨道上运行，则两颗运动星体的运动周期为         ；第二种形式是三颗星位于等边三角形的三个顶点上，并沿外接于等边三角形的圆形轨道运行，周期与第一种形式相同，则三颗星之间的距离为           。

地球同步卫星到地心的距离可用地球质量、地球自转周期与引力常量表示为=。

某行星绕太阳的运动可近似看作匀速圆周运动，已知行星运动的轨道半径为R，周期为T，万有引力恒量为G，则该行星的线速度大小为___________，太阳的质量可表示为__________。

为了验证地面上物体的重力与地球吸引月球、太阳吸引行星的力是否为同一性质的力，遵循同样的规律，牛顿曾经做过著名的月—地检验，其基本想法是：如果重力和星体间的引力是同一性质的力，都与距离的            关系，因为月心到地心的距离是地球半径的60倍，那么月球绕地球做近似圆周运动的向心加速度就应该是地面重力加速度的       倍，牛顿通过计算证明他的想法是正确的。

已知引力常量为G，地球的质量为M，地球自转的角速度为ω₀，月球绕地球转动的角速度为ω，假设地球上有一棵苹果树长到了接近月球那么高，则此树顶上一只苹果的线速度大小为___________，此速度___________（选填“大于”、“等于”或“小于”）月球绕地球运转的线速度。

在月球上以初速度v₀自高h处水平抛出的小球，射程可达s，已知月球半径为R，如果在月球上发射一颗月球的卫星，则它在月球表面附近环绕月球运动的周期    。

两颗人造卫星A、B 的质量之比m_A︰m_B = 1︰2 ，轨道半径之比r_A︰r_B = 1︰4 ，某一时刻它们的连线通过地心，则此时它们的线速度之比v_A︰v_B =        ，向心加速度之比
a_A︰a_B =         ，向心力之比F_A︰F_B =        。

月球质量大约是地球质量的1/81，若地球对月球的引力为F，则月球对地球的引力为： 　  。

两个大小相同的实心小铁球紧紧地靠在一起，它们之间的万有引力为F，若两个半径为小铁球半径2倍的实心大铁球紧靠在一起，则它们之间的万有引力为          .

据报道,最近在太阳系外发现了首颗“宜居”行星,其质量约为地球质量的6.4倍,一个在地球表面重量为600 N的人在这个行星表面的重量将变为960 N.由此可推知,该行星的半径是地球半径的_________倍

发现万有引力定律的科学家是    ，第一次通过实验比较准确的测出引力常量的科学家是       。

甲、乙两个质点间的万有引力大小为F，若甲物体的质量不变，乙物体的质量增加到原来的2倍，同时，它们之间的距离减为原来的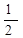，则甲、乙两物体间的万有引力大小将变为         。

银河系中有两颗行星绕某恒星运行，从天文望远镜中观察到它们的运转周期之比为27:1，则它们的轨道半径的比为___________________________。