高中物理万有引力定律及其应用填空题

已知月球绕地球运动周期T和轨道半径r，地球半径为R,万有引力常量为G.则地球的质量为       ，地球的平均密度为         。

设地球的质量为M，半径为R，则环绕地球飞行的第一宇宙速度v的表达式为______________；某行星的质量约为地球质量的1/4，半径约为地球半径的1/2，那么在此行星上的“第一宇宙速度”与地球上的第一宇宙速度之比为______________（已知万有引力常量为G）。

恒星演化发展到一定阶段，可能成为恒星世界的“侏儒”——中子星．中子星的半径较小，一般在7～20 km，但它的密度大得惊人．若某中子星的半径为10 km，密度为1.2×10¹⁷ kg/m³，那么该中子星上的第一宇宙速度约为________km/s

火星绕太阳做匀速圆周运动的周期为T，轨道半径为r，万有引力常量为G，则火星的线速度为v=____________、太阳的质量M=__________、火星的加速度为a=__________。

地球的半径约为R=6400千米，A、B两颗人造地球卫星沿圆轨道绕地球运行，它们离地球表面的高度分别为h_A=3600千米，h_B=1700千米，那末A、B两颗卫星的运行速率之比V_A:V_B=____________，运行周期之比T_A:T_B=____________。

某行星绕太阳的运动可近似看作匀速圆周运动，已知行星运动的轨道半径为R，周期为T，万有引力恒量为G，则该行星的线速度大小为_______,太阳的质量可表示为       .

火星与地球的质量之比为a，半径之比为b，则火星表面的重力加速度与地球表面的重力加速度之比为          

卡文迪许把他自己的实验说成是“称地球的重量”（严格地说应是“测量地球的质量”）。如果已知引力常量G、地球半径R和重力加速度g，那么我们就可以计算出地球的质量M=       ；如果已知某行星绕太阳运行所需的向心力是由太阳对该行星的万有引力提供的，该行星做匀速圆周运动，只要测出         和          就可以计算出太阳的质量。

自然界中任何两个物体都相互吸引，引力的大小与物体的质量m₁和m₂乘积成      ，与它们之间距离r的二次方成       。

有一行星密度为地球密度的一半，表面重力加速度为地球的2倍，则该行星质量为地球的_________倍，若地球同步卫星的高度为地球半径的6倍，该行星的同步卫星的高度为其半径的2.5倍，则该行星的自转周期为__________小时。

万有引力定律中引力常量：G=            N m²/kg²,由            第一次比较准确的测出。

地球半径为R，卫星A、B均环绕地球做匀速圆周运动，其中卫星A以第一宇宙速度环绕地球运动，卫星B的环绕半径为4R，则卫星A与卫星B的速度大小之比为________；周期之比为________。

一星球的半径为R，为了测量该星球两极和赤道的重力加速度及星球自转角速度，某人用小球在该星球表面做了以下实验：（不计小球在运动的过程中所受阻力）
①在该星球的两极（相当于地球的南极和北极），以初速度v₀（相对地面）从h高处将一小球水平抛出，小球触地时速度与水平方向成α角．则测量的该星球两极的重力加速度为            ；
②在该星球的赤道上（相当于地球的赤道），同样以速度v₀（相对地面）从h高处将一小球水平抛出，小球触地时速度与水平方向成β角．该星球赤道上的重力加速度为            ；该星球的自转角速度为               ．

地球的半径取6400km，某物在地面上所受地球引力为9×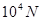，当它在距地面高度为12800km时，所受地球引力为__________N。

在某星球表面以初速度v₀坚直上抛一个物体，若物体只受该星球引力作用，物体上升的最大高度为h。该星球表面的重力加速度为      ；已知该星球的半径R，如果要在这个星球上发射一颗绕它运行的卫星，其做匀速圆周运动的最小周期为