高中物理万有引力定律及其应用计算题

2010年10月1日，我国成功发射了“嫦娥二号”探月卫星．“嫦娥二号”在距月球表面100 km高度的轨道上做圆周运动，这比“嫦娥一号”距月球表面200 km的圆形轨道更有利于对月球表面做出精细测绘．已知月球的质量约为地球质量的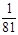，月球的半径约为地球半径的，地球半径为6400km，地球表面附近的重力加速度为9.8m/s²．求：

（1）月球表面附近的重力加速度；
（2）“嫦娥一号”与“嫦娥二号”在各自圆轨道上运行速度的大小之比．

高空遥感探测卫星在距地球表面高为h处绕地球转动，如果地球质量为M，地球半径为R，人造卫星质量为m，万有引力常量为G，求：
（1）人造卫星的角速度多大？
（2）人造卫星绕地球转动的周期是多少？
（3）人造卫星的向心加速度多大？

火箭载着宇宙探测器飞向某行星，火箭内平台上还放有测试仪器，如图所示。火箭从地面起飞时，以加速度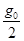竖直向上做匀加速直线运动(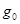为地面附近的重力加速度)，已知地球半径为R，升到某一高度时，测试仪器对平台的压力刚好是起飞时压力的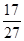，求此时火箭离地面的高度h。

一个质子由两个u夸克和一个d夸克组成。一个夸克的质量是7.1×10^-30kg，求两个夸克相距1.0×10^-16m时的万有引力。

若已知某行星的质量为m，该行星绕太阳公转的半径为r，公转周期为T，万有引力常量为G，则由此求出：该行星绕太阳公转的角速度ω太阳的质量M

某宇航员在地面上体重为600N，他在宇宙飞船中以5m/s²的加速度竖直匀加速上升，当上升到某高度时他所受的支持力为450N，求：①、宇航员的质量；②、此时宇宙飞船离地面的高度。（取地球半径6.4×10³km，地球表面处重力加速度10m/s²）

已知万有引力常量G，地球半径R₁，地球和太阳之间的距离r₁，地球绕太阳公转的周期T₁，月球半径R₂，地球和月亮之间的距离r₂，月球绕地球公转的周期T₂，地球表面的重力加速度g。请根据已知条件用二种估算方法地球的质量M。

两颗人造卫星A、B绕地球作匀速圆周运动，运动的周期之比为T_A：T_B=1：27，求：①、两卫星轨道半径之比；②、两卫星运动速率之比。

某人造地球卫星沿圆轨道运行，轨道半径是r，周期是T。试根据这些量推导出计算地球质量M的表达式。（引力常量为G）

“神州”六号飞船发射成功后，进入圆形轨道稳定运行，运转一周的时间为T，地球的半径为R，表面重力加速度为g，万有引力常量为G，试求：
（1）地球的密度；
（2）“神州”六号飞船轨道距离地面的高度。

宇宙飞船以a=g/2的加速度匀加速上升，由于超重现象，用弹簧秤测得质量为10kg的物体重量为75N，由此可求飞船所处位置距地面高度为多少？(地球半径R=6400km,g=10m/s²)

宇航员在月球上做竖直上抛运动的实验，将某物体由月球表面以初速度v₀释放，到达最大高度为h，设月球半径为R．据上述信息，求飞船在月球表面附近绕月球做匀速圆周运动所必须具有的速率.

神舟六号载人飞船在绕地球飞行了5 圈后变轨，轨道变为距地面高度为h 的圆形轨道．已知地球半径为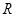，地面附近的重力加速度为．求：
(1)飞船在圆轨道上运行的速度；
(2)飞船在圆轨道上运行的周期．

如图所示，宇航员站在某星球表面上的斜面顶端A处，沿水平方向以初速度V₀抛出一个小球。经时间t小球落在斜面上的某一点B处。设空气阻力不计，该星球半径为R，万有引力常数为G。求该星球的质量M为多少（斜面倾角为θ）

已知“天宫一号”在地球上空的圆轨道上运行时离地面的高度为h，地球半径为R，地球表面的重力加速度为g．求：
（1）地球的密度为多少
（2）“天宫一号”在该圆轨道上运行时速度v的大小；