“嫦娥三号”的环月轨道可近似看成是圆轨道。观察“嫦娥三号”在环月轨道上的运动,发现每经过时间t通过的弧长为l,该弧长对应的圆心角为θ (弧度),如图所示。已知引力常量为G,由此可推导出月球的质量为( ) 
A. |
B. |
C. |
D. |
宇航员在地球表面以一定的初速度竖直上抛一小球,经过时间t落回原处;若在某星球表面以相同的速度竖直上抛一小球,则需经5t时间落回原处。已知该星半径与地球半径之比为1︰4,则( )
| A.该星表面重力加速度与地球表面重力加速度之比为5︰1 |
| B.该星质量与地球质量之比为1︰80 |
| C.该星密度与地球密度之比为4︰5 |
| D.该星的“第一宇宙速度”与地球的第一宇宙速度之比为1︰20 |
2013年1月27日,我国在境内再次成功地进行了陆基中段反导拦截技术试验,中段是指弹道导弹在大气层外空间依靠惯性飞行的一段.如图所示,一枚蓝军弹道导弹从地面上A点发射升空,目标是攻击红军基地B点,导弹升空后,红军反导预警系统立刻发现目标,从C点发射拦截导弹,并在弹道导弹飞行中段的最高点D将其击毁.下列说法中正确的是
| A.图中E到D过程,弹道导弹机械能不断增大 |
| B.图中E到D过程,弹道导弹的加速度不断减小 |
| C.弹道导弹在大气层外运动轨迹是以地心为焦点的椭圆 |
| D.弹道导弹飞行至D点时速度大于7.9 km/s |
气象卫星是用来拍摄云层照片、观测气象资料和测量气象数据的。我国先后自行成功研制和发射了“风云Ⅰ号”和“风云Ⅱ号”两颗气象卫星,“风云Ⅰ号”卫星轨道(极地圆轨道)与赤道平面垂直并且通过两极,绕地做匀速圆周运动的周期为12 h。“风云Ⅱ号”气象卫星轨道(地球同步轨道)平面在赤道平面内,绕地做匀速圆周运动的周期为24 h,则“风云Ⅱ号”卫星比“风云Ⅰ号”卫星( )
| A.轨道半径小 | B.线速度小 | C.角速度大 | D.向心加速度大 |
2011年8月,“嫦娥二号”成功进入了环绕“日地拉格朗日点”的轨道,我国成为世界上第三个造访该点的国家.如图所示,该拉格朗日点位于太阳和地球连线的延长线上,一飞行器处于该点,在几乎不消耗燃料的情况下与地球同步绕太阳做圆周运动,则此飞行器的
| A.线速度大于地球的线速度 |
| B.向心加速度大于地球的向心加速度 |
| C.向心力仅由太阳的引力提供 |
| D.向心力仅由地球的引力提供 |
如图所示,A为静止于地球赤道上的物体,B为绕地球沿椭圆轨道运行的卫星,C为绕地球做圆周运动的卫星,P为B、C两卫星轨道的交点.已知A、B、C绕地心运动的周期相同.相对于地心,下列说法中正确的是( )
A.物体A和卫星C具有相同大小的加速度
B.卫星C的运行速度大于物体A的速度
C.可能出现:在每天的某一时刻卫星B在A的正上方
D.卫星B在P点的运行加速度大小与卫星C在该点运行加速度大小相等
2013年12月2日1时30分,嫦娥三号探测器由长征三号乙运载火箭从西昌卫星发射中心发射,首次实现月球软着陆和月面巡视勘察。嫦娥三号的飞行轨道示意图如图所示。假设嫦娥三号在环月段圆轨道和椭圆轨道上运动时,只受到月球的万有引力,则( )
| A.若已知嫦娥三号环月段圆轨道的半径、运动周期和引力常量,则可算出月球的密度 |
| B.嫦娥三号由环月段圆轨道变轨进入环月段椭圆轨道时,应让发动机点火使其减速 |
| C.嫦娥三号在环月段椭圆轨道上P点的速度大于Q点的速度 |
| D.嫦娥三号在动力下降阶段,其引力势能减小 |
“嫦娥三号”飞船成功变轨,从100km的环月圆轨道I降低到椭圆轨道II(近月点15km、远月点100km),两轨道相交于点P,如图所示,关于“嫦娥三号”飞船,以下说法正确的是( )
| A.飞船在轨道I上运动到P点的速度比在轨道II上运动到P点的速度大 |
| B.飞船在轨道I上运动到P点的向心加速度比在轨道II上运动到P点的向心加速度小 |
| C.飞船在轨道I上的引力势能与动能之和比在轨道II上的引力势能与动能之和大 |
| D.飞船在轨道II上运动的周期大于在轨道I上运动的周期 |
如图所示,A是静止在赤道上的物体,随地球自转而做匀速圆周运动;B、C是同一平面内两颗人造卫星,B位于离地高度等于地球半径的圆形轨道上,C是地球同步卫星.已知第一宇宙速度为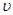 ,物体A和卫星B、C的线速度大小分别为
,物体A和卫星B、C的线速度大小分别为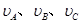 ,周期大小分别为TA、TB、TC,则下列关系正确的是
,周期大小分别为TA、TB、TC,则下列关系正确的是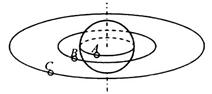
A.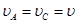 B.
B.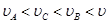
C.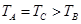 D.
D.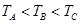
宇宙飞船绕地心做半径为r的匀速圆周运动,飞船舱内有一质量为m的人站在可称体重的台秤上,用R表示地球的半径,g表示地球表面处的重力加速度,g0表示宇宙飞船所在处的地球引力加速度,N表示人对秤的压力,则关于g0、N下面正确的是( )
A.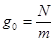 |
B.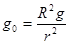 |
C.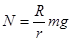 |
D.N=0 |
如图所示,飞行器P绕某星球做匀速圆周运动,星球相对飞行器的张角为θ,下列说法正确的是( )
| A.轨道半径越大,周期越长 |
| B.轨道半径越大,速度越大 |
| C.若测得周期和张角,可得到星球的平均密度 |
| D.若测得周期和轨道半径,可得到星球的平均密度 |
如图,三个质点a、b、c质量分别为m1、m2、M(M>> m1,M>> m2)。在c的万有引力作用下,a、b在同一平面内绕c沿逆时针方向做匀速圆周运动,它们的周期之比Ta∶Tb=1∶k。从图示位置开始,在b运动一周的过程中
| A.a、b距离最近的次数为k次 |
| B.a、b距离最近的次数为k-1次 |
| C.a、b、c共线的次数为2k |
| D.a、b、c共线的次数为2k-2 |
据报道,中俄双方将联合对火星及其卫星“火卫一”进行探测。“火卫一”位于火星赤道正上方,到火星中心的距离为9450km。“火卫一”绕火星1周需7h39min。若其绕行轨道可认为是圆形轨道,引力常量为G,由以上信息不能确定的是( )
| A.火卫一的质量 | B.火星的质量 |
| C.火卫一的绕行速度 | D.火卫一的向心加速度 |