高中物理万有引力定律及其应用试题

科技馆中，有一个模拟万有引力的装置。在如图1所示的类似锥形漏斗固定的容器中，有两个小球在该容器表面上绕漏斗中心轴做水平圆周运动，其运行能形象地模拟了太阳系中星球围绕太阳的运行。图2为示意图，图3为其模拟的太阳系运行图。图2中离中心轴的距离相当于行星离太阳的距离。

（1）在图3中，设行星A₁和B₁离太阳距离分别为r₁和r₂，求A₁和B₁运行速度大小之比。
（2）在图2中，若质量为m的A球速度大小为v，在距离中心轴为x₁的轨道面上旋转，由于受到微小的摩擦阻力，A球绕轴旋转同时缓慢落向漏斗中心。当其运动到距离中心轴为x₂的轨道面时，两轨道面之间的高度差为H。求此过程中A球克服摩擦阻力所做的功。

如图所示，从地面上A点发射一枚远程弹道导弹，假设导弹仅在地球引力作用下，沿ACB椭圆轨道飞行击中地面目标B，C为轨道的远地点，距地面高度为h。已知地球半径为R，地球质量为M，引力常量为G，则下列结论正确的是（    ）

A．导弹在C点的速度大于	B．导弹在C点的速度等于
C．导弹在C点的加速度等于	D．导弹在C点的加速度大于

某课外小组经长期观测，发现靠近某行星周围有众多卫星，且相对均匀地分布于行星周围，假设所有卫星绕该行星的运动都是匀速圆周运动，通过天文观测，测得离行星最近的一颗卫星的运动半径为R₁，周期为T₁，已知万有引力常为G。求：
⑴行星的质量；
⑵若行星的半径为R，行星的第一宇宙速度；
⑶通过天文观测，发现离行星很远处还有一颗卫星，其运动半径为R₂，周期为T₂，试估算靠近行星周围众多卫星的总质量(提示:研究很远的卫星可把其他卫星和行星整体作为中心天体)。

我国“神舟”九号宇宙飞船已经发射成功，当时在飞船控制中心的大屏幕上出现的一幅卫星运行轨迹图，如图所示，它记录了“神舟”六号飞船在地球表面垂直投影的位置变化；图中表示在一段时间内飞船绕地球圆周飞行四圈，依次飞经中国和太平洋地区的四次轨迹①、②、③、④，图中分别标出了各地点的经纬度（如：在轨迹①通过赤道时的经度为西经157.5°，绕行一圈后轨迹②再次经过赤道时经度为180°……），若地球半径为R=6400km，地球表面处的重力加速度g=10m/s²，从图中的信息计算“神舟”九号宇宙飞船的
（1）运行周期    （2）飞船离地面的高度

北斗导航系统又被称为“双星定位系统”，具有导航、定位等功能。计划“北斗”系统最终将有5颗静止轨道卫星和30颗非静止轨道卫星组成。这些卫星均绕地心O做匀速圆周运动。某时刻两颗正在同时提供服务的非静止轨道卫星分别位于轨道上的A、B两位置（如图所示）．若卫星均顺时针运行，轨道半径为，地球表面处的重力加速度为g，地球半径为R，不计卫星间的相互作用力．则以下判断中错误的是（  )

A．这两颗卫星的加速度大小相等，均为
B．卫星1由位置A运动到位置B所需的时间为
C．卫星1由位置A运动到位置B的过程中万有引力做功为零
D．卫星1向后喷气就一定能追上卫星2

如图所示，方框表示绕地球做匀速圆周运动的航天站中的一个实验室，质量为m、受地球的吸引力为G的物体A放在P平面上，引力G的方向与P平面垂直。设物体A与P平面的动摩擦因数为，现在A物体上加一个沿P平面方向的力F，则以下结论不正确的是（  ）

A．实验室观察到A物体的加速度为

B．实验室观察到A物体的加速度为

C．A物体绕地球做圆周运动的向心加速度为

D．A物体的加速度大小为

假设太阳系内某行星和地球的公转轨道均为圆形，且在同一平面内，如图所示，半径较小的轨道是某行星公转的轨道，半径较大的轨道是地球公转的轨道。在地球上观测，发现该行星与太阳可呈现的视角（太阳与行星均看成质点，它们与眼睛连线的夹角）有最大值，并且最大视角的正弦值为16/25.则该行星的公转周期为多少年？

如图，三个质点a、b、c质量分别为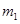、、（）。在c的万有引力作用下，a、b在同一平面内绕c沿逆时针方向做匀速圆周运动，轨道半径之比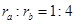,则它们的周期之比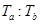=______;从图示位置开始，在b运动一周的过程中，a、b、c共线了____次。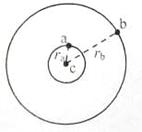

如图所示，从地面上的A点发射一枚远程弹道导弹，在引力作用下沿着ACB椭圆轨道飞行击中地面上的目标B点，C点为轨道的远地点，C点距地面高度为h。已知地球半径为R，地球质量为M，万有引力常量为G。设离地面高度为h的圆形轨道上的卫星运动的周期为T₀，下面论述正确的是                                      

A．导弹在点的速度大于

B．导弹在点的加速度等于

C．地球球心为导弹椭圆轨道的一个焦点

D．导弹从A点到B 点的时间一定小于T0

某恒星远处有一颗行星，靠近行星周围有众多的卫星，且相对均匀地分布于行星周围。假设卫星绕行星的运动是匀速圆周运动，通过天文观测，测得离该行星最近的一颗卫星运动的轨道半径为，周期为。已知万有引力常量为G。
（1）求该行星的质量；
（2）通过天文观测，发现离该行星很远处还有一颗卫星，其运动的轨道半径为，周期为，试估算该行星周围众多卫星的总质量。
（3）通过天文观测发现，某一时刻行星跟距离自己最近的卫星以及距离自己很远的卫星正好分布在一条直线上，求再经过多长时间它们又将分布在一条直线上。

2012年我国宣布北斗导航系统正式商业运行。北斗导航系统又被称为“双星定位系统”，具有导航、定位等功能。“北斗”系统中两颗工作星均绕地心O做匀速圆周运动，轨道半径为r，某时刻两颗工作卫星分别位于轨道上的A、B两位置（如图）．若卫星均顺时针运行，地球表面处的重力加速度为，地球半径为R，不计卫星间的相互作用力．则以下判断中正确的是（  ）

A．这两颗卫星的加速度大小相等，均为

B．卫星l由位置A运动至位置B所需的时间为

C．卫星l向后喷气就一定能追上卫星2

D．卫星1由位置A运动到位置B的过程中万有引力做正功

飞船记录显示地球赤道上有一个物体随地球自转而做圆周运动，所受的向心力为F₁，向心加速度为a₁，线速度为v₁，角速度为；绕地球表面附近做圆周运动的人造卫星所受的向心力为F₂，向心加速度为a₂，线速度为v₂，角速度为；地球同步卫星所受的向心力为F₃，向心加速度为a₃，线速度为v₃，角速度为；地球表面和的重力加速度为g，第一宇宙速度为v，假设三者质量相等，则（   ）

A．F1＝F2＞F3	B．a1＝a2＝g＞a3
C．v1＝v2＝v＞v3	D．＝＜

天文学家将相距较近、仅在彼此的引力作用下运行的两颗恒星称为双星。双星系统在银河系中很普遍。经观测某双星系统中两颗恒星A、B围绕它们连线上的某一固定点分别做匀速圆周运动，周期均为T。已知恒星A、B之间的距离为L，A、B的质量之比2 ：1，万有引力常量为G，求：
(1) 恒星A做匀速圆周运动的轨道半径R_A；
(2) 双星的总质量M 。

如图所示，是某次同步卫星发射过程的示意图，先将卫星送入一个近地圆轨道，然后在P点点火加速，进入椭圆转移轨道，其中P是近地点，Q是远地点，在Q点再次点火加速进入同步轨道。设卫星在近地圆轨道的运行速率为v₁，加速度大小为a₁；在P点短时间点火加速之后，速率为v₂，加速度大小为a₂；沿转移轨道刚到达Q点速率为v₃，加速度大小为a₃；在Q点点火加速之后进入圆轨道，速率为v₄，加速度大小为a₄，则(    )

A．	B．
C．	D．

假如一个做匀速圆周运动的人造地球卫星的轨道半径增大到原来的2倍，仍做匀速圆周运动，则（     ）

A．根据公式，可知卫星的线速度增大到原来的2倍

B．根据公式，可知卫星所需的向心力减小到原来的

C．根据公式，可知地球提供的向心力将减小到原来的

D．根据上述B和C给出的公式，可知卫星的线速度将减小到原来的