如图6—5—2所示，直径为d的纸质圆筒，以角速度ω绕轴O高速运动，有一颗子弹沿直径穿过圆筒，若子弹穿过圆筒时间小于半个周期，在筒上先、后留下a、b两个弹孔，已知ao、bo间夹角为φ弧度，则子弹速度是多少？
如图6—5—6所示，小球Q在竖直平面内做匀速圆周运动，当Q球转到图示位置时，有另一小球P在距圆周最高点为h处开始自由下落，要使两球在圆周最高点相碰，则Q球的角速度ω应满足什么条件？
如图甲所示，将质量为m的两个小球（可看成质点），用长为L的两根细软线拴连，线的上端连于O点且绕O点自由转动时与竖直方向夹角为θ。
如图乙所示，将其中一质量为m的小球仍与一长为L的细绳连接，放在表面光滑的正圆锥体表面，上端可绕圆锥顶点自由转动。圆锥体放在水平面上，其轴线沿竖直方向，圆锥母线与轴线之间夹角α为30°，试求：（1）图甲中小球圆周运动的周期T=？（2）图乙中当正圆锥体沿水平x轴方向匀加速运动的加速度a多大时，小球刚要离开锥面？（3）将图乙中与小球相连的细线穿过圆锥顶端的光滑小圆环后,与放在倾角β=37°的对称斜槽（斜槽两平面材料相同，与竖直面都成30°）里的质量为M的圆柱体相连，连接圆柱的细线平行斜槽的棱，如图丙所示。当小球以速度v=
绕圆锥轴线做水平匀速圆周运动而圆柱M不动时，圆柱与两接触面间的摩擦因数μ至少多大？
求：（l）推导第一宇宙速度v1的表达式；
（2）若卫星绕地球做匀速圆周运动，运行轨道距离地面高度为h，求卫星的运行周期T。
（1）已知第一种形式中的每颗恒星质量均为m，正方形边长为L，求其中一颗恒星受到的合力；
（2）已知第二种形式中的两外侧恒星质量均为m、两内侧恒星质最均为M ，四颗恒星始终位于同一直线，且相邻恒星之间距离相等，求内侧恒星质量M与外侧恒质m的比值。
有一个圆盘能够在水平面内绕其圆心O匀速旋转，盘的边缘为粗糙平面（用斜线表示）其余为光滑平面。现用很轻的长L="5" cm的细杆连接A、B两个物体(看做质点)，A、B的质量分别为mA="0.1" kg和mB="0.5" kg，B放在圆盘的粗糙部分，A放在圆盘的光滑部分。并且细杆指向圆心，A离圆心O为10cm，如图所示,当圆盘以n=2转/秒的转速转动时，A和B能跟着一起作匀速圆周运动。（
）求:
（1）B受到的摩擦力的大小。
（2）细杆所受的作用力。
钢铁质量为
的超重车，行驶在半径为厅的圆弧形拱桥顶点，已知此处桥面能承受的最大压力只是车重的
倍；要使车能安全沿桥面行驶，求在此处车的速度应在什么范围内？
如图所示，一个光滑的圆锥体固定在水平圆盘上，其轴线沿竖直方向并与圆盘中心重合，母线与轴线之间的夹角为θ. 一条长为L的细绳，一端固定在圆锥体的顶点O处，另一端拴着一质量为m的小球（可视为质点）. 现让圆锥体绕其中心轴线由静止开始转动，求当其角速度由零增大到
且稳定时的过程中，细绳的拉力对小球所做的功.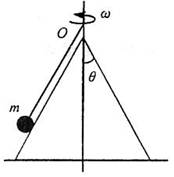
OA杆是机器带动绕其轴线旋转的竖直杆，细绳的一端固定在杆的A点，另一端系一质量m="1" kg的小球，绳长为L="1" m.开始小球绕轴线在水平面内做匀速圆周运动，细绳与竖直杆的夹角为θ1=30°.现使机器转速加大，使小球在另一水平面内做稳定的匀速圆周运动时，细绳与竖直杆的夹角为θ2=60°.求此过程中机器对小球所做的功.（取g="10" m/s2）
如图2，用手握着一绳端在水平桌面上做半径为r的匀速圆周运动，圆心为O，角速度为ω。绳长为l，方向与圆相切，质量可以忽略。绳的另一端系着一个质量为m的小球，恰好也沿着一个以O点为圆心的大圆在桌面上运动，小球和桌面之间有摩擦，试求：
⑴ 手对细绳做功的功率P；
⑵ 小球与桌面之间的动摩擦因数μ。
如图所示，在绕竖直轴匀速转动的水平圆盘盘面上，离轴心r=20cm处放置一小物块A，其质量为m＝2kg，A与盘面间相互作用的静摩擦力的最大值为其重力的k倍（k＝0.5），试求
⑴当圆盘转动的角速度ω＝2rad/s时，物块与圆盘间的摩擦力大小多大？方向如何？
⑵欲使A与盘面间不发生相对滑动，则圆盘转动的最大角速度多大？（取g=10m/s2）
长为L的细线，拴一质量为m的小球，一端固定于O点，让其在水平面内做匀速圆周运动（这种运动通常称为圆锥摆运动），如图所示，当摆线L与竖直方向的夹角是α时，求：
（1）线的拉力F；
（2）小球运动的线速度的大小；
（3）小球运动的角速度及周期。
如图所示，半径为R的圆板做匀速运动，当半径OB转到某一方向时，在圆板中心正上方h处以平行于OB方向水平抛出一球，小球抛出时的速度及圆盘转动的角速度为多少时，小球与圆盘只碰撞一次，且落点为B。
粤公网安备 44130202000953号
