高中物理匀速圆周运动计算题

在如图所示的圆锥摆(小球在水平面内做匀速圆周运动)中，已知绳子长度为L，绳子转动过程中与竖直方向的夹角为θ ，试求小球做圆周运动的速率。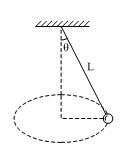

如图，光滑水平桌面上，弹簧一端固定在O点，另一端系一质量的小球，使小球绕O点做匀速圆周运动。已知弹簧原长，劲度系数，小球做圆周运动的角速度，求小球做匀速圆周运动时弹簧长度。

如图8所示的结构装置可绕竖直轴转动，假若细绳长L=0.2m，水平杆长L₀=0.1m，小球的质量m=0.3kg.求：
（1）使绳子与竖直方向夹角45⁰角，该装置以多大角速度转动才行？
（2）此时绳子的拉力为多大？

旋转秋千是游乐园里常见的游乐项目，它有数十个座椅通过缆绳固定在旋转圆盘上，每一座椅可坐一人。启动时，座椅在旋转圆盘的带动下围绕竖直的中心轴旋转飘游，如图甲所示，我们把这种情况抽象为图乙的模型：一质量m=40kg的球通过长L=12.5m的轻绳悬于竖直面内的直角杆上，水平杆长L′=7.5m。整个装置绕竖直杆转动，绳子与竖直方向成角。当θ =37°时，（g = 9.8m/s²，sin37°= 0.6，cos37°= 0.8）求：
（1）绳子的拉力大小；
（2）该装置转动的角速度。

A、B两物体都做匀速圆周运动，A的质量是B的质量的一半，A的轨道半径是B轨道半径的一半，当A转过60°角时时间内，B转过了45°角，则
（1）A物体的向心加速度与B的向心加速度之比为多少？
（2）A物体的向心力与B的向心力之比为多少？

(8分)如图7所示，一水平放置的半径为r = 0．5m的薄圆盘绕过圆心O点的竖直轴转动，圆盘边缘有一质量m = 1．0kg的小滑块（可看成是质点）。当圆盘转动的角速度达到某一数值时，滑块从圆盘边缘滑落，滑块与圆盘间的动摩擦因数μ = 0．2，圆盘所水平面离水平地面的高度h = 2．5m，g取10m/s²．

（1）当圆盘的角速度多大时，滑块从圆盘上滑落？
（2）若取圆盘所在平面为零势能面，求滑块到达地面时的机械能；

如图所示，m₁、m₂是质量分别为50g和100g的小球，套在水平光滑杆上。两球相距2l cm，并用细线连接．欲使两球绕轴以600 r／min的转速在水平面内转动而不滑动，两球离转动中心分别为多远?线上拉力是多大?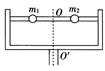

如图所示，质量为M＝1.0Kg的物体A置于可绕竖直轴匀速转动的平台上。物体A用细绳通过光滑的定滑轮与质量为m＝0.4Kg的物体B相连，物体B悬于空中。假定A与轴O的距离r＝0.5m，A与平台间的最大静摩擦力为重力的0.3倍。（g取10m/s²），求：
（1）物体A与圆盘保持相对静止且不受摩擦力时，平台的角速度ω₀；
（2）为使物体A与圆盘相对静止，圆盘匀速转动的角速度的大小范围。

如右图所示,质量是1 kg的小球用长为0.5 m的细线悬挂在O点,O点距地面高度为1m, 如果使小球绕OO′轴在水平面内做圆周运动,若细线最大承受拉力为12.5 N,求:
（1）当小球的角速度为多大时,线将断裂.
（2）断裂后小球落地点与悬点的水平距离.（g="10" m/s²）

如图所示，半径为R的球壳，内壁光滑，当球壳绕竖直方向的中心轴转动时，一个小物体恰好相对静止在球壳内的P点，OP连线与竖直轴夹角为θ．试问：球壳转动的周期多大？