旋转秋千是游乐园里常见的游乐项目,它有数十个座椅通过缆绳固定在旋转圆盘上,每一座椅可坐一人。启动时,座椅在旋转圆盘的带动下围绕竖直的中心轴旋转飘游,如图甲所示,我们把这种情况抽象为图乙的模型:一质量m=40kg的球通过长L=12.5m的轻绳悬于竖直面内的直角杆上,水平杆长L′=7.5m。整个装置绕竖直杆转动,绳子与竖直方向成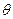 角。当θ =37°时,(g = 9.8m/s2,sin37°= 0.6,cos37°= 0.8)求:
角。当θ =37°时,(g = 9.8m/s2,sin37°= 0.6,cos37°= 0.8)求:
(1)绳子的拉力大小;
(2)该装置转动的角速度。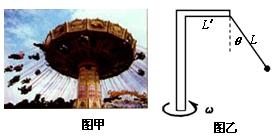
旋转秋千是游乐园里常见的游乐项目,它有数十个座椅通过缆绳固定在旋转圆盘上,每一座椅可坐一人。启动时,座椅在旋转圆盘的带动下围绕竖直的中心轴旋转飘游,如图甲所示,我们把这种情况抽象为图乙的模型:一质量m=40kg的球通过长L=12.5m的轻绳悬于竖直面内的直角杆上,水平杆长L′=7.5m。整个装置绕竖直杆转动,绳子与竖直方向成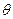 角。当θ =37°时,(g = 9.8m/s2,sin37°= 0.6,cos37°= 0.8)求:
角。当θ =37°时,(g = 9.8m/s2,sin37°= 0.6,cos37°= 0.8)求:
(1)绳子的拉力大小;
(2)该装置转动的角速度。