高中物理匀速圆周运动试题

【原创】对做匀速圆周运动的物体，下列关于其向心加速度的说法中正确的是（  ）

A．根据知，向心加速度由速度和轨道半径决定

B．向心加速度的大小保持不变，但向心加速度时刻在变

C．向心加速度的方向时刻指向圆心，所以方向保持不变

D．向心加速度描述速度的方向变化的快慢

物体在做匀速圆周运动过程中，其向心加速度

A．大小、方向均保持不变	B．大小、方向均时刻改变
C．大小时刻改变、方向保持不变	D．大小保持不变，方向时刻改变

如图所示，一个小球绕圆心O做匀速圆周运动，已知圆周半径为r，该小球运动的角速度大小为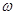，则它运动线速度的大小为

A．

B．

C．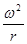

D．

对于做匀速圆周运动的质点，下列说法正确的是：（   ）

A．根据公式a=v^2/r， 可知其向心加速度a与半径r成反比

B．根据公式a=ω^2r， 可知其向心加速度a与半径r成正比

C．根据公式ω=v/r， 可知其角速度ω与半径r成反比

D．根据公式ω=2πn，可知其角速度ω与转速n成正比

如图所示，在固定的圆锥形漏斗的光滑内壁上，有两个小物块A和B，质量分别为m_A和m_B，它们分别紧贴漏斗的内壁。在不同的水平面上做匀速圆周运动，则以下叙述正确的是

A.不论A、B质量关系如何，物块A的线速度始终大于物块B的线速度
B.只有当m_A＜m_B，物块A的角速度才会大于物块B的角速度
C.不论A、B质量关系如何，物块A对漏斗内壁的压力始终大于物块B对漏斗内壁的压力
D.不论A、B质量关系如何，物块A的周期始终大于物块B的周期

人造地球卫星进入轨道做匀速圆周运动，下面说法正确的是（     ）

A．卫星内的物体失重，卫星本身没失重	B．卫星内的物体不再受地球引力作用
C．卫星内物体仍受地球引力作用	D．卫星内的物体没有地球引力作用而有向心力作用

小球做匀速圆周运动，半径为R，向心加速度为a，则下列说法错误的是(    )

A．小球的角速度	B．小球运动的周期
C．t时间内小球通过的路程	D．t时间内小球转过的角度

如图所示，甲、乙两快艇在湖面上做匀速圆周运动。关于两快艇的运动，下列说法正确的是（     ）

A．若两快艇运动的周期相等，半径较小的向心加速度较大

B．若两快艇运动的线速度大小相等，半径较小的向心加速度较大

C．若两快艇运动的角速度相等，半径较小的向心加速度较大

D．若两快艇运动的线速度大小相等，半径较大的向心加速度较大

如图所示，BC是半径为R的竖直面内的圆弧轨道，轨道末端C在网心O的正下方，∠BOC= 60°，将质量为m的小球，从与O等高的A点水平抛出，小球恰好从B点沿圆弧切线方向进入网轨道，由于小球与圆弧之间有摩擦，能够使小球从B到C做匀速圆周运动。重力加速度大小为g.则

A．从B到C,小球克服摩擦力做功为
B．从B到C,小球与轨道之间的动摩擦因数可能保持不变
C. A、B两点间的距离为
D．在C点,小球对轨道的压力为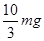

如图，两个质量均为m的小木块a和b（可视为质点）放在水平圆盘上，a与转轴OO′的距离为l，b与转轴的距离为2l。木块与圆盘的最大静摩擦力为木块所受重力的k倍，重力加速度大小为g。若圆盘从静止开始绕转轴缓慢地加速转动，用ω表示圆盘转动的角速度，下列说法正确的是： （     ）

A．b一定比a先开始滑动

B．a、b所受的摩擦力始终相等

C．ω＝是b开始滑动的临界角速度

D．当ω＝时，a所受摩擦力的大小为kmg

如图所示，两平行金属板间距为d，电势差为U，板间电场可视为匀强电场；金属板下方有一磁感应强度为B的匀强磁场。带电量为+q、质量为m的粒子，由静止开始从正极板出发，经电场加速后射出，并进入磁场做匀速圆周运动。忽略重力的影响，求：

（1）匀强电场的电场强度E的大小。
（2）粒子从电场射出时速度v的大小。
（3）粒子在磁场中做匀速圆周运动的半径R。

某原子电离后其核外只有一个电子，若该电子在核的静电力作用下绕核做匀速圆周运动，那么电子运动（ ）

A．半径越大，加速度越大	B．半径越小，周期越大
C．半径越大，角速度越小	D．半径越小，线速度越小

在绕地球作匀速圆周运动的太空仓内，按照同学们使用的新人教版教材要求，能完成的实验是：

A．验证力的平行四边形法则

B．探究弹簧形变量与弹力的关系

C．探究物体加速度与质量和合外力的关系

D．用平抛运动测初速度

如图所示为某一皮带传动装置．主动轮的半径为r₁，从动轮的半径为r₂.已知主动轮做顺时针转动，转速为n，转动过程中皮带不打滑．下列说法正确的是 (　　)．

A．从动轮做顺时针转动

B．从动轮做逆时针转动

C．从动轮的转速为n

D．从动轮的转速为n

两物体做匀速圆周运动，其运动半径之比为2：3，受到向心力之比为3：2，则其动能比为（   ）

A．9：4

B．4：9

C．1：1

D．2：3