高中物理平抛运动计算题

山谷中有三块大石头和一根不可伸长的青藤，其示意图如下。图中A、B、C、D均为石头的边缘点，O为青藤的固定点，h₁=1.8m，h₂=4.0m，x₁=4.8m，x₂=8.0m。开始时，质量分别为M=10kg和m=2kg的大小两只金丝猴分别位于左边和中间的石头上，当大猴发现小猴将受到伤害时，迅速从左边石头A点起水平跳到中间石头，大猴抱起小猴跑到C点，抓住青藤的下端荡到右边石头的D点，此时速度恰好为零。运动过程中猴子均看成质点，空气阻力不计，重力加速度g=10m/s²，求：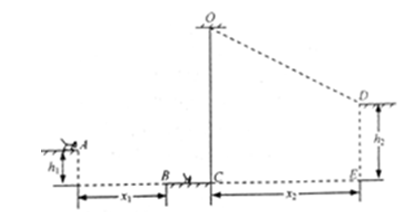

（1）大猴子水平跳离的速度最小值
（2）猴子抓住青藤荡起时的速度大小
（3）荡起时，青藤对猴子的拉力大小

如图所示，水平传送带的速度为4.0m/s，它的右端与等高的光滑水平平台相接触。一工件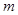（可看成质点）轻轻放在传送带的左端，工件与传送带间的动摩擦因数μ=0.3，经过一段时间工件从光滑水平平台上滑出，恰好落在小车左端，已知平台与小车的高度差h=0.8，小车左端距平台右端的水平距离为s=1.2m，取g=10m/s²，求：

（1）工件水平抛出的初速度v₀是多少？
（2）传送带的长度L是多少？

如图所示，在水平地面上空有一架飞机在进行投弹训练，飞机沿水平方向做匀加速直线运动．当飞机飞经观察点B点正上方A点时投放一颗炸弹，经时间T炸弹落在观察点B正前方L₁处的C点，与此同时飞机投放出第二颗炸弹，最终落在距观察点B正前方L₂处的D点，且L₂＝3L₁，空气阻力不计．求：

(1)飞机水平飞行的加速度；
(2)第二次投弹时飞机的速度及在两次投弹间隔T时间内飞机飞行距离.

【改编】如图所示，位于竖直平面上半径为R=0.2m的1/4圆弧轨道AB光滑无摩擦，O点为圆心。质量为m=1kg的小球从A点由静止释放，到达B点时，小球对轨道的压力为30N，从B点飞出，最后落在地面C处。若BC所连直线与水平方向夹角为θ，且tanθ=1，取g ="10" m/s²，不计空气阻力，求：

（1）小球通过B点时的速度；
（2）B点与水平地面的高度差H；
（3）小球落地时的速度大小。

一条水平放置的水管，横截面积S=1.0cm²，距离地面高度h=3.6m，水从管口以不变的速度源源不断地沿水平方向射出，水落地的位置到管口的水平距离是0.9m。设管口横截面上各处水的速度都相同，空中的水的体积是多少？（g=10 m/s²，不计空气阻力）

如图，置于圆形水平转台边缘的小物块随转台加速转动，当转速达到某一数值时，物块恰好滑离转台开始做平抛运动．现测得转台半径R＝0.5 m，离水平地面的高度H＝0.8 m，物块平抛落地过程水平位移的大小s＝0.4 m．设物块所受的最大静摩擦力等于滑动摩擦力，取重力加速度g＝10 m/s².求：

（1）物块做平抛运动的初速度大小v₀；
（2）物块与转台间的动摩擦因数μ.

(9分) 如图所示，水平轨道AB与竖直半圆形光滑轨道在B点平滑连接，半圆形轨道半径R=2.5m，质量m=0.1kg的小滑块（可视为质点）以一定的速度从水平轨道进入半圆形轨道，沿轨道运动恰好能到最高点C，且从C点水平飞出后恰好落在A点，重力加速度g=10m/s²，试分析求解：

(1)滑块通过C点时的速度大小；
(2)AB间的距离x。

水平抛出的一个石子，经过0.4s落到地面，落地时的速度方向跟水平方向的夹角是53°。试求：
（1）石子的抛出点距地面的高度；
（2）石子抛出的水平初速度。

滑草逐渐成为我们浙江一项新兴娱乐活动。某体验者乘坐滑草车运动过程简化为如图所示，滑草车从A点静止滑下，滑到B点时速度大小不变而方向变为水平，再滑过一段水平草坪后从C点水平抛出，最后落在三角形状的草堆上。已知斜坡AB与水平面的夹角θ=37°，长为x_AB=15m，水平草坪BC长为x_BC=10m。从A点滑到了B点用时3s。该体验者和滑草车的质量m=60kg，运动过程中看成质点，在斜坡上运动时空气阻力不计。（sin37°=0.6，cos37°=0.8，重力加速度g=10m/s²）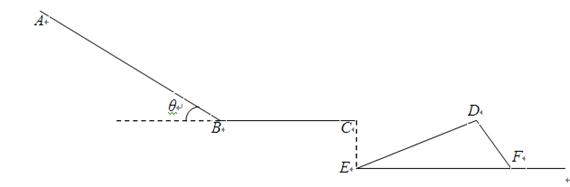

（1）求滑草车和草坪之间的动摩擦因数；
（2）体验者滑到水平草坪时，恰好受到与速度方向相反的水平恒定风的作用，风速大小为5m/s，已知风的阻力大小F与风速v满足经验公式F=1.2v²。求体验者滑到C点时的速度大小；
（3）已知三角形的草堆的最高点D与C点等高，且距离C点6m，其左顶点E位于C点正下方3m处。在某次滑草过程中，体验者和滑草车离开C点时速度大小为7m/s，无风力作用，空气阻力忽略不计，求体验者和滑草车落到草堆时的动能。

如图所示为水上滑梯的简化模型：倾角θ=37°斜滑道AB和水平滑道BC平滑连接，起点A距水面的高度H=7m，BC长d=2m，端点C距水面的高度h=1m。质量m=50kg的运动员从滑道起点A点无初速地自由滑下，运动员与AB、BC间的动摩擦因数均为μ=0.1。已知cos37°=0.8，sin37°=0.6，运动员在运动过程中可视为质点，g取10 m/s²。求：

（1）运动员从A滑到C的过程中克服摩擦力所做的功W；
（2）运动员到达C点时的速度大小υ；
（3）保持水平滑道端点在同一竖直线上，调节水平滑道高度h和长度d到图中B′C′ 位置时，运动员从滑梯平抛到水面的水平位移最大，求此时滑道B′C′距水面的高度h′．

如图所示，光滑的圆弧轨道与倾角为θ=37°的斜面相切于B点，圆弧轨道的半径为R=1m，质量为M=2kg的物块甲在斜面上A点由静止释放，物块甲与斜面的动摩擦因数为μ=0.25，AB间距离为s=4m，当甲运动到C点时，恰好与迎面过来的质量m=0.5kg的乙相碰，碰后两者粘在一起，向左运动，恰好能到达圆弧轨道的最高点D点，（已知sin37°=0.6，cos37°=0.8，g取10m/s²）求：

（1）物块甲与物块乙相碰前的速度v₁；
（2）物块甲和乙碰撞后的一瞬间，它们对圆弧轨道最低点C的压力之和；
（3）两物块从D点抛出后，落到斜面上所用的时间．

如图所示为水上滑梯的简化模型：倾角θ=37°斜滑道AB和水平滑道BC平滑连接，起点A距水面的高度H=7m，BC长d=2m，端点C距水面的高度h=1m。质量m=50kg的运动员从滑道起点A点无初速地自由滑下，运动员与AB、BC间的动摩擦因数均为μ=0.1。已知cos37°=0.8，sin37°=0.6，运动员在运动过程中可视为质点，g取10 m/s²。求：

（1）运动员从A滑到C的过程中克服摩擦力所做的功W；
（2）运动员到达C点时的速度大小υ；
（3）保持水平滑道端点在同一竖直线上，调节水平滑道高度h和长度d到图中B′C′ 位置时，运动员从滑梯平抛到水面的水平位移最大，求此时滑道B′C ′ 距水面的高度h′。

(15分) 如图所示，水平轨道AB与竖直半圆形光滑轨道在B点平滑连接，AB段长x=10m，半圆形轨道半径R=2.5m，质量m=0.1kg的小滑块（可视为质点）以一定的速度从水平轨道进入半圆形轨道，沿轨道运动到最高点C，从C点水平飞出。若小滑块从C点水平飞出后恰好落在A点，重力加速度g=10m/s²，试分析求解：

(1)滑块通过C点时的速度大小；
(2)滑块刚进入半圆形轨道时，在B点对轨道的压力大小；

(13分)如图所示，一工件置于水平地面上，其AB段为一半径R＝1.0 m的光滑圆弧轨道，BC段为一长度L＝0.5 m的粗糙水平轨道，二者相切于B点，整个轨道位于同一竖直平面内，P点为圆弧轨道上的一个确定点．一可视为质点的物块，其质量m＝0.2 kg，与BC间的动摩擦因数μ₁＝0.4。工件质量M＝0.8 kg，与地面间的动摩擦因数μ₂＝0.1。(取g＝10 m/s²)

(1)若工件固定，将物块由P点无初速度释放，滑至C点时恰好静止，求P、C两点间的高度差h.
(2)若将一水平恒力F作用于工件，使物块在P点与工件保持相对静止，一起向左做匀加速直线运动．
①求F的大小．
②当速度v＝5m/s时，使工件立刻停止运动(即不考虑减速的时间和位移)，物块飞离圆弧轨道落至BC段，求物块的落点与B点间的距离。

如图所示，遥控赛车比赛中的一个规定项目是“飞跃壕沟”，比赛要求是：赛车从起点出发，沿水平直轨道运动，在B点飞出后越过“壕沟”，落在平台EF段．已知赛车的额定功率P=12.0W，赛车的质量m=1.0kg，在水平直轨道上受到的阻力f=2.0N，AB段长L=10.0m，B、E两点的高度差h=1.25m，BE的水平距离x=1.5m．赛车车长不计，空气阻力不计.g取10m/s²．

（1）若赛车在水平直轨道上能达到最大速度，求最大速度v_m的大小；
（2）要使赛车越过壕沟，求赛车在B点速度至少多大；
（3）若比赛中赛车以额定功率运动，经过A点时速度v_A=1m/s，求赛车在A点时加速度大小．