高中物理平抛运动计算题

在500米的高空，有一架飞机以40 m/s的速度水平匀速飞行，若忽略空气阻力的影响，取g＝10m/s²，tan37°=3/4
求：（1）从飞机上掉下来的物体，经多长时间落到地面；
（2）物体从掉下到落地，水平方向移动的距离多大；
（3）从掉下开始，第3秒末物体的速度。

(8分)如图所示，质量为m的小球从A点水平抛出，抛出点距离地面高度为H，不计空气的粘滞阻力对小球运动的影响，重力加速度为g。在无风情况下小球的落地点B到抛出点的水平距离为L；当有恒定的水平风力F时，小球仍以原初速度抛出，落地点C到抛出点的水平距离为3L/4，求：

（1）小球初速度的大小；
（2）水平风力F的大小；

如图所示，跳台滑雪运动员经过一段加速滑行后从O点水平飞出，经3.0 s落到斜坡上的A点．已知O点是斜坡的起点，斜坡与水平面的夹角θ＝37°，运动员的质量m＝50 kg.不计空气阻力．(取sin 37°＝0.60，cos 37°＝0.80，g取10 m/s²)求：
(1)A点与O点的距离L；
(2)运动员离开O点时的速度大小．

同学们在学习了平抛运动知识后，对体育课推铅球的运动进行了研究。某男同学身高1.8m，现以水平初速度把铅球平推出去，测得他推铅球成绩是：若把球的运动看作是平抛运动，球平推出的高度近似看作等于人的身高，g取，求：
（1）球被推出时的初速度的大小；
（2）球落地的末速度的大小。

水平抛出的一个石子，经过0.4 s落到地面，落地时的速度方向跟水平方向的夹角是53°，（g取10 m/s²，sin53°=0.8，cos53°=0.6）求：
（1）石子的抛出点距地面的高度；
（2） 石子抛出的水平初速度；
（3）石子落地点距抛出点的水平距离。

如图所示，轨道ABCD位于同一竖直平面内，AB段是光滑的四分之一的圆弧轨道，BC段是高H=3.2m、倾角θ=45°的斜面，CD段是足够长的水平轨道．一小球从AB轨道的某点由静止开始下滑，并从B点水平飞出，不计空气阻力，取g=10m/s²．

（1）若小球从B点飞出后恰好落在C点，求此情形小球在B点的速度大小v_B和释放点到B点的高度h₀；
（2）若释放点到B点的高度h₁=1.8m，求小球第一次落到轨道前瞬间速度方向与水平面夹角α的正切值；
（3）若释放点到B点的高度h₂=0.2m，求小球第一次落到轨道的位置到B点的距离L．

如图所示，一光滑的半径为R的半圆形轨道放在水平面上，一个质量为m的小球以某一速度冲上轨道，当小球将要从轨道口飞出时，轨道的压力恰好为零，则小球落地点C距A处多远?

如图所示，在水平地面上固定一倾角θ＝37°、表面光滑且足够长的斜面体，物体A以v₁＝6m/s的初速度沿斜面上滑，同时在物体A的正上方，有一物体B以某一初速度水平抛出．如果当A上滑到最高点时恰好被B物体击中．（A、B均可看作质点，sin37°＝0.6，cos37°＝0.8，取g＝10m/s²）求：

（1）物体A上滑到最高点所用的时间t；
（2）物体B抛出时的初速度v₂；
（3）物体A、B间初始位置的高度差h．

如图所示，半径R=0.2m的光滑四分之一圆轨道MN竖直固定放置，末端N与一长L=0.8m的水平传送带相切，水平衔接部分摩擦不计，传动轮（轮半径很小）作顺时针转动，带动传送带以恒定的速度ν₀运动．传送带离地面的高度h=1.25m，其右侧地面上有一直径D=0.5m的圆形洞，洞口最左端的A点离传送带右端的水平距离S=1m，B点在洞口的最右端．现使质量为m=0.5kg的小物块从M点由静止开始释放，经过传送带后做平抛运动，最终落入洞中，传送带与小物块之间的动摩擦因数μ=0.5． g取10m/s²．求：

（1）小物块到达圆轨道末端N时对轨道的压力
（2）若ν₀=3m/s，求物块在传送带上运动的时间
（3）若要使小物块能落入洞中，求ν₀应满足的条件．

如图所示，一小球（可视为质点）自平台上水平抛出，恰好落在临近平台的一倾角为α＝37°的斜面顶端，并刚好沿斜面下滑，已知斜面顶端与平台的高度差h＝0.45 m，求：
（重力加速度g取10 m/s²，sin37°＝0.6，cos 37°＝0.8）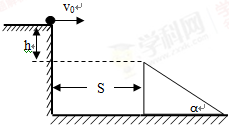

（1）小球水平抛出的初速度v₀是多少？
（2）斜面顶端与平台边缘的水平距离s是多少？

如图所示，P是固定在水平面上的圆弧轨道，O是圆弧的圆心，C为圆弧轨道最高点，D为圆弧轨道最低点。从高台变B点以速度v₀水平飞出质量为m、带电量为+q的小球，恰能从圆弧轨道的左端A点沿圆弧切线方向进入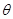，是OA与竖直方向的夹角。圆弧轨道的竖直直径COD右边存在竖直向下的匀强电场，电场强度为E，已知：m=1kg。V0=3m/s，q=，，，g=10m/s2,sin370=0.6， cos370=0.8.若小球恰能到达最高点C，不计空气阻力和所有摩擦，求：

（1）A、B两点的高度差
（2）圆弧轨道的半径R的大小

如图所示，一个半径R=1.0m的圆弧形光滑轨道固定在竖直平面内，轨道的一个端点B和圆心O的连线与竖直方向夹角，C为轨道最低点，D为轨道最高点，一个质量m=0.50kg的小球（视为质点）从空中A点以的速度水平抛出，恰好从轨道的B端沿切线方向进入轨道，重力加速度，试求：

（1）小球抛出点A距圆弧轨道B端的高度h
（2）小球经过轨道最低点C时对轨道的压力
（3）小球能否到达轨道最高点D？若能到达，试求对D点的压力，若不能到达，试说明理由

如图所示，天花板上有固定转轴O，长为L的轻杆一端可绕转轴O在竖直平面内自由转动，另一端固定一质量为M的小球。一根不可伸长的足够长轻绳绕过定滑轮A，一端与小球相连，另一端挂着质量为m₁的钩码，定滑轮A的位置可以沿OA连线方向调整。小球、钩码均可看作质点，不计一切摩擦，g取10m/s²。

（1）若将OA间距调整为L，则当轻杆与水平方向夹角为30º时小球恰能保持静止状态，求小球的质量M与钩码的质量m₁之比；
（2）若在轻绳下端改挂质量为m₂的钩码，且M:m₂=4:1，并将OA间距调整为L，然后将轻杆从水平位置由静止开始释放，求小球与钩码速度大小相等时轻杆与水平方向的夹角θ；
（3）在（2）的情况下，测得杆长L=2.175m，仍将轻杆从水平位置由静止开始释放，当轻杆转至竖直位置时，小球突然与杆和绳脱离连接而向左水平飞出，求当钩码上升到最高点时，小球与O点的水平距离。

如图所示，飞机离地面高度为H=500m，飞机的水平飞行速度为v₁=100m/s，追击一辆速度为v₂=20m/s同向行驶的汽车，欲使炸弹击中汽车，飞机应在距离汽车的水平距离多远处投弹？(不考虑空气阻力)

在1125m的高空有一驾飞机以50m/s的速度水平飞行（g取10m/s²）
求：（1）从飞机上掉下的物体经多长时间落地？
（2）物体从掉下到落地，水平方向移动的距离多大？