高中物理平抛运动试题

如图所示，在倾角为30⁰的斜面上，质量为0.1kg的小球从斜面上的A点水平抛出落在斜面上的B点，测得AB之间的距离为S=0.4m，空气阻力不计，那么下列说法正确的是（   ）

A．小球从A点抛出到B过程重力做功为0.2J

B．若取A点为零势能位置，小球在A点的重力势能小于B点重力势能

C．小球从A点抛出到B点的时间为0.2s

D．小球从A点运到到B点过程中机械能增加

特战队员在进行素质训练时，抓住一端固定在同一水平高度的不同位置的绳索，从高度一定的平台由水平状态无初速开始下摆，如图所示，在到达竖直状态时放开绳索，特战队员水平抛出直到落地。不计绳索质量和空气阻力，特战队员可看成质点。下列说法正确的是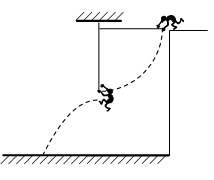

A．绳索越长，特战队员落地时的水平位移越大

B．绳索越长，特战队员在到达竖直状态时绳索拉力越大

C．绳索越长，特战队员落地时的水平速度越大

D．绳索越长，特战队员落地时的速度越大

如图所示，x轴沿水平方向，y轴沿竖直方向，OM是与x轴成θ角的一条射线.现从坐标原点O以速度v₀水平抛出一个小球，小球与射线OM交与P点，此时小球的速度v与OM的夹角为α，若保持方向不变而将小球初速度增大为2v₀，小球与射线OM交与P'，此时小球的速度v与OM的夹角为α'，则（ ）

A．小球从O运动到P'的时间是从O到P时间的2倍

B．夹角α'是α的2倍

C．小球通过P'点的速度为4v

D．OP'=4OP

如图所示，将a、b两小球以大小为20 m/s的初速度分别从A、B两点相差1 s先后水平相向抛出，a小球从A点抛出后，经过时间t，a、b两小球恰好在空中相遇，且速度方向相互垂直，不计空气阻力，取g＝10 m/s²，则抛出点A、B间的水平距离是（　　）

A．80 m       B．100 m           C．200 m          D．180 m

如图所示，在一次空地演习中，距离水平地面高度为H的飞机以水平速度v_l发射一枚炮弹欲轰炸地面目标P，反应灵敏的地面拦截系统同时以速度v₂竖直向上发射炮弹拦截。设拦截系统与飞机的水平距离为S，若拦截成功，不计空气阻力，下列说法正确
的是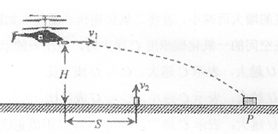

A．两者相遇时间

B．两者相遇时间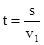

C．两者速度关系满足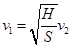

D．两者速度关系满足v1 = v2

一艘客轮因故障需迅速组织乘客撤离。乘客在甲板上须利用固定的绳索下滑到救援快艇上。绳索与竖直方向的夹角θ＝37°，设乘客下滑过程绳索始终保持直线。为保证行动又快又安全，乘客先从静止开始匀加速滑到某最大速度，再匀减速滑至快艇，速度刚好为零，加速过程与减速过程中的加速度大小相等。在乘客开始下滑时，船员同时以水平速度向快艇抛出救生圈刚好落到救援快艇上（快艇可视为质点），如图所示。并知乘客下滑的时间是救生圈平抛下落的2倍，不计空气阻力，重力加速度g取10 m/s²，sin37°= 0.6，cos37°= 0.8，求：

（1）乘客沿着绳索下滑的时间t；
（2）乘客下滑过程的最大速度v_m。

如图所示竖直面内光滑轨道，它是由半径为R的半圆环和切于D点的水平部分组成．a、b、c三个物体由水平部分向半环滑去，它们重新落回到水平面上时的落点到切点D的距离依次为AD＜2R，BD=2R，CD＞2R．若a、b、c三个物体离开半环在空中飞行时间依次为t_a、t_b、t_c，则关于三者的时间关系一定有（  ）    

A．ta=tb

B．tc=ta

C．tb=tc

D．无法确定

一人用一根长L=1m，最大只能承受T=46N拉力的轻绳子，拴着一个质量m=1kg的小球（不考虑其大小），在竖直平面内作圆周运动，已知圆心O离地高H=21m，如图所示，若小球运动到达最低点时绳刚好被球拉断，求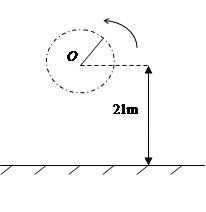

（1）小球到达最低点的速度大小是多少?   
（2）小球落地点到O点的水平距离是多少?（g=10m/s²）

）如图所示，某人骑摩托车在水平道路上行驶，要在A处越过x=5m的壕沟，沟面对面比A处低h=1.25m，（取g=10m/s²）求：

（1）摩托车在空中飞行的时间？
（2）摩托车的开始飞越壕沟的初速度至少要有多大？

（1）平抛物体的运动规律可以概括为两点：①水平方向做匀速运动，②竖直方向做自由落体运动。为了研究平抛物体的运动，可做下面的实验：如图5所示，用小锤打击弹性金属片，A球就水平飞出，同时B球被松开，做自由落体运动，两球同时落到地面，这个实验（     ）

A．只能说明上述规律中的第①条

B．只能说明上述规律中的第②条

C．不能说明上述规律中的任何一条

D．能同时说明上述两条规律

（2）在做研究平抛运动的实验时，让小球多次沿同一轨道运动，通过描点法画出小球平抛运动的轨迹。如图是用一张印有小方格的纸记录轨迹，小方格的边长为L，小球在平抛运动途中的几个位置如图中的a、b、c、d所示，则由图可知小球从a运动到b和b运动到c的时间是       （填”相等”或”不相等”）的, 小球平抛的初速度的计算式为v₀=      （用L、g表示）。

如图所示，轨道ABCD的AB段为一半径R=0.2的光滑1/4圆形轨道，BC段为高为h=5的竖直轨道，CD段为水平轨道。一质量为0.1的小球由A点从静止开始下滑到B点时速度的大小为2/s，离开B点做平抛运动（g取10/s²），求：

（1）小球离开B点后，在CD轨道上的落地点到C的水平距离
（2）小球到达B点时对圆形轨道的压力；
（3）如果在BCD轨道上放置一个倾角＝45°的斜面（如图中虚线所示），那么小球离开B点后能否落到斜面上？如果能，求它第一次落在斜面上的位置。

横截面为直角三角形的两个相同斜面紧靠在一起，固定在水平面上，如图所示．它们的竖直边长都是底边长的一半．现有三个小球从左边斜面的顶点以不同的初速度向右平抛，最后落在斜面上．其落点分别是a、b、c.下列判断正确的是(　　)

A．图中三小球比较，落在a点的小球飞行时间最短

B．图中三小球比较，落在c点的小球飞行过程速度变化最大

C．图中三小球比较，落在c点的小球飞行过程速度变化最快

D．无论小球抛出时初速度多大，落到两个斜面上的瞬时速度都不可能与斜面垂直

在某次自由式滑雪比赛中，一运动员从弧形雪坡上沿水平方向飞出后，又落回到斜面雪坡上，如图所示，若斜面雪坡的倾角为θ，飞出时的速度大小为v₀，不计空气阻力，运动员飞出后在空中的姿势保持不变，重力加速度为g，则

A．运动员在空中经历的时间是

B．运动员落到雪坡时的速度大小是

C．如果v0不同，则该运动员落到雪坡时的速度方向也就不同

D．不论v0多大，该运动员落到雪坡时的速度方向都是相同的

如图所示，从倾角为α的斜面上的某点先后将同一小球以不同的初速水平抛出，均落到斜面上，当抛出的速度为v₁时，小球到达斜面时速度方向与斜面的夹角为θ₁，当抛出的速度为v₂时，小球到达斜面时速度方向与斜面的夹角为θ₂，若不考虑空气阻力，则（　　）

A．θ1可能大于θ2	B．θ1可能小于θ2
C．θ1一定等于θ2	D．θ1、θ2的大小关系与斜面的倾角α无关

如图所示在倾角为37°的斜面上，从A点以20 m/s的初速度水平抛出一个小球，小球落在B点。求小球在空中飞行的时间t和A、B两点间的距离s．(g＝10 m/s²，sin 37°＝0.6，cos 37°＝0.8)