在足够大的光滑水平桌面上,一质量m=1kg的小球静止在图示坐标系的原点O处。从t=0时刻起,小球受到沿+x方向的大小为F1=2N的恒定拉力作用开始运动。在t=1s时刻,撤去F1,立即换成沿+y方向的大小为F2=2N的恒定拉力作用在物体上。在t=2s时刻,把F2也撤去。在t=3s时刻,小球开始进入一个固定在水平桌面上的圆形光滑细管道(在图上只画了该管道的管口,管道的内径略微大于小球的直径)。已知小球是沿管道的切线方向进入管道的,且已知该管道的圆心在y轴上。求:
(1)t=2s时刻,小球的位置坐标
(2)进入管道后,小球对管道水平方向上作用力的大小
(3)沿着管道,小球第一次到达y轴的位置
质量为0.2kg的小球固定在长为0.9m的轻杆一端,杆可绕O点的水平轴在竖直平面内转动。(g=10 m/s2)求:
(1)当小球在最高点的速度多大时,球对杆的作用力为零?
(2)当小球在最高点的速度分别为6m/s和1.5m/s时,球对杆的作用力。
一种巨型娱乐器械由升降机送到离地面75m的高处,然后让座舱自由落下。落到离地面30 m高时,制动系统开始启动,座舱均匀减速,到地面时刚好停下。若座舱中某人用手托着M=5Kg的铅球,取g=10m/s2,试求
(1)从开始下落到最后着地经历的总时间多长?
(2)当座舱落到离地面35m的位置时,手对球的支持力是多少?
(3)当座舱落到离地面15m的位置时,球对手的压力是多少?
在2008年北京残奥会开幕式上,运动员手拉绳索向上攀登,最终点燃了主火炬,体现了残疾运动员坚忍不拔的意志和自强不息的精神。为了探究上升过程中运动员与绳索和吊椅间的作用,可将过程简化。一根不可伸缩的轻绳跨过轻质的定滑轮,一端挂一吊椅,另一端被坐在吊椅上的运动员拉住,如图所示。设运动员的质量为65kg,吊椅的质量为15kg,不计定滑轮与绳子间的摩擦。重力加速度取。当运动员与吊椅一起正以加速度上升时,试求:
(1)运动员竖直向下拉绳的力; (2)运动员对吊椅的压力。
如图所示,底座A上装有0.5 m长的直立杆,底座和杆的总质量为M=0.2 kg,杆上套有质量为0.05 kg的小环B,它与杆之间有摩擦.当环从底座上以4 m/s的初速度飞起时,刚好能达到杆顶而没有脱离直立杆,取g=10 m/s2.
求:在环升起过程中,底座对水平面的压力为多大?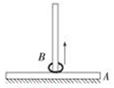
如图,支架质量为M,置于水平地面上。轴O处有一长为L的杆(质量不计),杆的另一端固定一个质量为m的小球。使小球在竖直平面上作匀速圆周运动,支架保持静止。若小球到达最高点时恰好对支架的压力为0,则: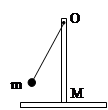
(1)小球的速度大小为多少?
(2)小球经过最低点时支架对地面的压力为多大 ?
如图所示,质量为0.2kg的物体带正电,其电量为4×10-3C,从半径为0.3m光滑的1/4圆弧滑轨上端A点由静止下滑到底端B点,然后继续沿水平面滑动。物体与水平面间的滑动摩擦因数为0.4,整个装置处于E=103N/C的竖直向下的匀强电场中。(g取10m/s2)求: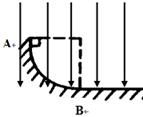
(1)物体运动到圆弧滑轨底端B点时对轨道的压力;
(2)物体在水平面上滑行的最大距离。
如图所示,传送带的两个轮子半径均为r=0.2m,两个轮子最高点A、B在同一水平面内,A、B间距离L=5m,半径R=0.4m的固定、竖直光滑圆轨道与传送带相切于B点,C点是圆轨道的最高点.质量m=0.1kg的小滑块与传送带之间的动摩擦因数μ=0.4,重力加速度g=10m/s2.求:
(1)传送带静止不动,小滑块以水平速度v0滑上传送带,并能够运动到C点,v0至少多大?
(2)当传送带的轮子以w=10rad/s的角速度转动时,将小滑块无初速地放到传送带上的A点,小滑块从A点运动到B点的时间t是多少?
(3)传送带的轮子以不同的角速度匀速转动,将小滑块无初速地放到传送带上的A点,小滑块运动到C点时,对圆轨道的压力大小不同,最大压力Fm是多大?
(15分)如图9所示,一辆卡车后面用轻绳拖着质量为m的物体A,A与地面的摩擦不计.
图9
(1)当卡车以a1= g的加速度运动时,绳的拉力为
g的加速度运动时,绳的拉力为 mg,则A对地面的压力为多大?
mg,则A对地面的压力为多大?
(2)当卡车的加速度a2=g时,绳的拉力为多大?
(15分)一个箱子放在水平地面上,箱内有一固定的竖直杆,在杆上套着一个环,箱与杆的质量为M,环的质量为m,如图8所示.已知环沿杆匀加 速下滑时,环与杆间的摩擦力大小为Ff,则此时箱对地面的压力大小为多少? 
(14分)如图16所示,光滑匀质圆球的直径d=40 cm,质量为M=20 kg,悬线长L=30 cm,正方形物块A的厚度b=10 cm,质量为m=2 kg,物块A与墙之间的动摩擦因数μ=0.2.现将物块A轻放于球和墙之间后放手,取g=10 m/s2,求:
(1)墙对A的摩擦力为多大?
(2)施加一个与墙面平行的外力于物体A上,使物体A在未脱离圆球前贴着墙
沿水平方向做加速度a=5 m/s2的匀加速直线运动,那么这个外力的大小和方
向如何?
(12分)雨滴接近地面的过程可以看做匀速直线运动,此时雨滴的速度称为收尾速度.某同学在一本资料上看到,雨滴的收尾速度v与雨滴的半径r成正比,由此该同学对雨滴运动中所受的阻力F作了如下几种假设:
(1)阻力只与雨滴的半径成正比,即F=kr(k为常数).
(2)阻力只与速度的平方成正比,即F=kv2(k为常数).
(3)阻力与速度的平方和半径的乘积成正比,即F=krv2(k为常数).
你认为哪种假设能够解释雨滴收尾速度与半径成正比这一关系?请写出推导过程.
(12分)如图15所示,光滑小圆环A吊着一个重为G1的砝码套在另一个竖直放置的大圆环上,今有一细绳拴在小圆环A上,另一端跨过固定在大圆环最高点B处的一个小滑轮后吊着一个重为G2的砝码,如果不计小环、滑轮、绳子的重量大小.绳子又不可伸长,求平衡时弦AB所对的圆心角θ.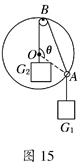
(10分)如图14所示,轻杆BC的C点用光滑铰链与墙壁固定,杆的B点通过水平细绳AB使杆与竖直墙壁保持30°的夹角.若在B点悬挂一个定滑轮(不计重力),某人用它匀速地提起重物.已知重物的质量m=30 kg,人的质量M=50 kg,g取10 m/s2.试求:
(1)此时地面对人的支持力的大小;
(2)轻杆BC和绳AB所受力的大小.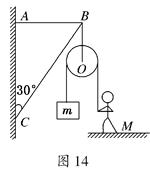
如图所示,一辆卡车后面用轻绳拖着质量为m的物体A,A与地面的摩擦不计.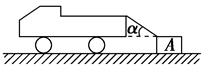
(1)当卡车以a1=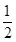 g的加速度运动时,绳的拉力为
g的加速度运动时,绳的拉力为 mg,则A对地面的压力为多大?
mg,则A对地面的压力为多大?
(2)当卡车的加速度a2=g时,绳的拉力为多大?