如图所示,QB段为一半径为 的光滑圆弧轨道,AQ段为一长度为
的光滑圆弧轨道,AQ段为一长度为 的粗糙水平轨道,两轨道相切于Q点,Q在圆心O的正下方,整个轨道位于同一竖直平面内。物块
的粗糙水平轨道,两轨道相切于Q点,Q在圆心O的正下方,整个轨道位于同一竖直平面内。物块 的质量为m=1kg(可视为质点),P与AQ间的动摩擦因数
的质量为m=1kg(可视为质点),P与AQ间的动摩擦因数 ,若物块
,若物块 以速度v0从A点滑上水平轨道,到C点后又返回A点时恰好静止。(取
以速度v0从A点滑上水平轨道,到C点后又返回A点时恰好静止。(取 )求:
)求:
(1)v0的大小;
(2)物块P第一次刚通过Q点时对圆弧轨道的压力。
某同学表演魔术时,将一小型条形磁铁藏在自己的袖子里,然后对着一悬挂的金属小球指手画脚,结果小球在他神奇的“功力”下飘动起来.假设当隐藏的小磁铁位于小球的左上方某一位置C(∠QCS=30°)时,金属小球偏离竖直方向的夹角θ也是30°,如图所示.已知小球的质量为m,该同学(含磁铁)的质量为M,求此时: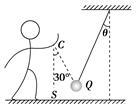
(1)悬挂小球的细线的拉力大小为多少?
(2)该同学受到地面的支持力和摩擦力大小各为多少?
如图所示,质量M=2 kg的滑块套在光滑的水平轨道上,质量m=1 kg的小球通过长L=0.5 m的轻质细杆与滑块上的光滑轴O连接,小球和轻杆可在竖直平面内绕O轴自由转动,开始轻杆处于水平状态,现给小球一个竖直向上的初速度v0=4 m/s,g取10 m/s2。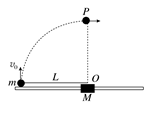
(1)若锁定滑块,试求小球通过最高点P时对轻杆的作用力大小和方向;
(2)解除对滑块的锁定,小球过最高点时速度大小v′=2 m/s,求此时滑块的速度大小。
(10分)在2008年北京残奥会开幕式上,运动员手拉绳索向上攀登,最终点燃了主火炬,体现了残疾运动员坚忍不拔的意志和自强不息的精神。为了探究上升过程中运动员与绳索和吊椅间的作用,可将过程简化。一根不可伸缩的轻绳跨过轻质的定滑轮,一端挂一吊椅,另一端被坐在吊椅上的运动员拉住,如图所示。设运动员的质量为65kg,吊椅的质量为15kg,不计定滑轮与绳子间的摩擦。重力加速度取g=10m/s2。当运动员与吊椅一起正以加速度a=1m/s2上升时,试求: 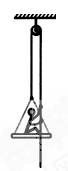
(1)运动员竖直向下拉绳的力;
(2)运动员对吊椅的压力。
如图所示,小球被轻质细绳系住斜吊着放在光滑斜面上,小球与斜面均处于静止状态,设小球质量m=2 kg,斜面倾角α=30°,细绳与竖直方向夹角θ=30°,光滑斜面体的质量M=3 kg,置于粗糙水平面上.(g取10 m/s2)求: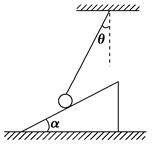
(1)细绳对小球拉力的大小;
(2)地面对斜面体的摩擦力的大小和方向.
如图所示,固定在水平面上的斜面其倾角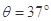 ,长方形木块A的MN面上钉着一颗钉子,质量m=1.5kg的小球B通过一细线与小钉子相连接,细线与斜面垂直。木块与斜面间的动摩擦因数
,长方形木块A的MN面上钉着一颗钉子,质量m=1.5kg的小球B通过一细线与小钉子相连接,细线与斜面垂直。木块与斜面间的动摩擦因数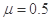 。现将木块由静止释放,木块与小球将一起沿斜面下滑。求在木块下滑的过程中;(取g=l0m/s2)
。现将木块由静止释放,木块与小球将一起沿斜面下滑。求在木块下滑的过程中;(取g=l0m/s2)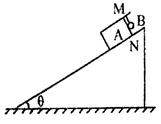
(1)木块与小球的共同加速度的大小;
(2)小球对木块MN面的压力的大小和方向。
游乐园的小型“摩天轮”上对称站着质量均为m的8位同学,如图所示,“摩天轮”在竖直平面内逆时针匀速转动,若某时刻转到顶点a上的甲同学让一小重物做自由落体运动,并立即通知下面的同学接住,结果重物掉落时正处在c处(如图)的乙同学恰好在第一次到达最低点b处接到,己知“摩天轮”半径为R,重力加速度为g,(不计人和吊篮的大小及重物的质量).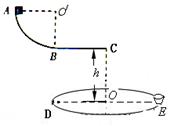
问:(1)接住前重物下落运动的时间t="?" (2)人和吊篮随“摩天轮”运动的线速度大小v=? (3)乙同学在最低点处对地板的压力FN=?
如图所示,光滑绝缘的细圆管弯成半径为R的半圆形,固定在竖直面内,管口B、C的连线水平.质量为m的带正电小球从B点正上方的A点自由下落,A、B两点间距离为4R。从小球(小球直径小于细圆管直径)进入管口开始,整个空间中突然加上一个斜向左上方的匀强电场,小球所受电场力在竖直方向上的分力方向向上,大小与重力相等,结果小球从管口C处离开圆管后,又能经过A点. 设小球运动过程中电荷量没有改变,重力加速度为g,求: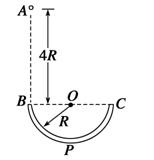
(1)小球到达B点时的速度大小;
(2)小球受到的电场力大小;
(3)小球经过管口C处时对圆管壁的压力.
石墨烯是近些年发现的一种新材料,其超高强度及超强导电、导热等非凡的物理化学性质有望使21世纪的世界发生革命性的变化,其发现者由此获得2010年诺贝尔物理学奖。用石墨烯制作超级缆绳,人类搭建"太空电梯"的梦想有望在本世纪实现。科学家们设想,通过地球同步轨道站向地面垂下一条缆绳至赤道基站,电梯仓沿着这条缆绳运行,实现外太空和地球之间便捷的物资交换。

(1)若"太空电梯"将货物从赤道基站运到距地面高度为的同步轨道站,求轨道站内质量为
的货物相对地心运动的动能。设地球自转角速度为
,地球半径为
。
(2)当电梯仓停在距地面高度的站点时,求仓内质量
的人对水平地板的压力大小。取地面附近重力加速度
,地球自转角速度
,地球半径
。
如图所示,竖直固定放置的粗糙斜面AB的下端与光滑的圆弧BCD的B点相切,圆弧轨道的半径为R,圆心O与A、D在同一水平面上,∠COB=θ.现有质量为m的小物体从距D点为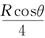 的高处无初速释放,已知物体恰能从D点进入圆轨道,求:
的高处无初速释放,已知物体恰能从D点进入圆轨道,求: 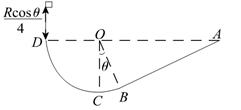
(1)为使小物体不会从A点冲出斜面,小物体与斜面间的动摩擦因数至少为多少?
(2)若小物块与斜面间的动摩擦因数μ=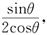 则小物体在斜面上通过的总路程为多少?
则小物体在斜面上通过的总路程为多少?
(3)在(2)的条件下,当小物体通过圆弧轨道最低点C时,对C的最大压力和最小压力各是多少?
(15分)如图,一不可伸长的轻绳上端悬挂于O点,下端系一质量m=1.0kg的小球。现将小球拉到A点(保持绳绷直)由静止释放,当它经过B点时绳恰好被拉断,小球平抛后落在水平地面上的C点。地面上的D点与OB在同一竖直线上,已知绳长L=1.0m,B点离地高度H=1.0m,A、B两点的高度差h=0.5m,重力加速度g取10m/s2,不计空气阻力影响,求: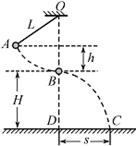
⑴地面上DC两点间的距离s;⑵轻绳所受的最大拉力大小。
如图所示,AB段为一半径R=0.2m的光滑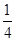 圆弧轨道,EF为一倾角是37°的足够长的光滑固定斜面,斜面上有一质量为0.1kg的薄木板CD,开始时木板被锁定.一质量也为0.1kg的物块从A点由静止开始下滑,通过B点后水平抛出,经过一段时间后恰好以平行于木板的方向滑上木板,在物块滑上木板的同时,木板解除锁定,下滑过程中某时刻物块和木板能达到共同速度.已知物块与木板间的动摩擦因数为
圆弧轨道,EF为一倾角是37°的足够长的光滑固定斜面,斜面上有一质量为0.1kg的薄木板CD,开始时木板被锁定.一质量也为0.1kg的物块从A点由静止开始下滑,通过B点后水平抛出,经过一段时间后恰好以平行于木板的方向滑上木板,在物块滑上木板的同时,木板解除锁定,下滑过程中某时刻物块和木板能达到共同速度.已知物块与木板间的动摩擦因数为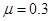 (g取
(g取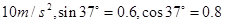 ),
),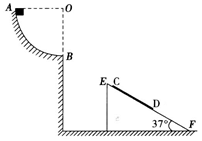
求:(1)物块到达B点时对圆弧轨道压力的大小;
(2)物块做平抛运动的时间;
(3)若下滑过程中某时刻物块和木板达到共同速度,则这个速度为多大?(木板足够长)
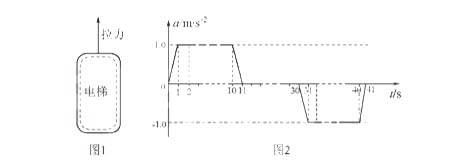
摩天大楼中一部直通高层的客运电梯,行程超过百米。电梯的简化模型如1所示。考虑安全、舒适、省时等因索,电梯的加速度a是随时间t变化的。已知电梯在t = 0时由静止开始上升,a - t图像如图2所示。电梯总质最m = 2.0× kg。忽略一切阻力,重力加速度g取10m/s2。
kg。忽略一切阻力,重力加速度g取10m/s2。
(1)求电梯在上升过程中受到的最大拉力F1和最小拉力F2;
(2)类比是一种常用的研究方法。对于直线运动,教科书中讲解了由v - t图像求位移的方法。请你借鉴此方法,对比加速度的和速度的定义,根据图2所示a - t图像,求电梯在第1s内的速度改变量△v1和第2s末的速率v2;
(3)求电梯以最大速率上升时,拉力做功的功率p:再求在0~11s时间内,拉力和重力对电梯所做的总功W。