如图所示,在xoy平面内,三个半径为a 的四分之一圆形有界区域Ⅰ、Ⅱ、Ⅲ内有垂直纸面向外、磁感应强度为B的匀强磁场(含边界上)。一群质量为m电荷量为q的带正电的粒子同时从坐标原点O以相同的速率、不同的方向射入第一象限内(含沿x轴、y轴方向),它们在磁场中运动的轨道半径也为a,在y≤-a的区域,存在场强为E、沿-x方向的匀强电场。整个装置在真空中,不计粒子的重力及粒子之间的相互作用。求:
(1)粒子从O点射入磁场时的速率v0;
(2)这群粒子从O点射入磁场至运动到x轴的最长时间;
(3)这群粒子到达y轴上的区域范围。
如图所示,在xOy平面内,以O1(0,R)为圆心、R为半径的圆形区域内有垂直平面向里的匀强磁场B1,x轴下方有一直线ab,ab与x轴相距为d,x轴与直线ab间区域有平行于y轴的匀强电场E,在ab的下方有一平行于x轴的感光板MN,ab与MN间区域有垂直于纸平面向外的匀强磁场B2。在0≤y≤2R的区域内,质量为m、电荷量为e的电子从任何位置从圆形区域的左侧沿x轴正方向以速度v0射入圆形区域,经过磁场B1偏转后都经过O点,然后进入x轴下方。已知x轴与直线ab间匀强电场场强大小 ,ab与MN间磁场磁感应强度
,ab与MN间磁场磁感应强度 。不计电子重力。
。不计电子重力。
(1)求圆形区域内磁场磁感应强度B1的大小?
(2)若要求从所有不同位置出发的电子都不能打在感光板MN上,MN与ab板间的最小距离h1是多大?
(3)若要求从所有不同位置出发的电子都能打在感光板MN上,MN与ab板间的最大距离h2是多大?当MN与ab板间的距离最大时,电子从O点到MN板,运动时间最长是多少?
如图所示,斜面体ABC放在水平桌面上,其倾角为37º,其质量为M=5kg。现将一质量为m=3kg的小物块放在斜面上,并给予其一定的初速度让其沿斜面向上或者向下滑动。已知斜面体ABC并没有发生运动,重力加速度为10m/s2,sin37º=0.6。则关于斜面体ABC受到地面的支持力N及摩擦力f的大小,下面给出的结果可能的有( )
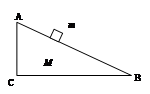
| A.N=50N,f=40N | B.N=87.2N,f=9.6N |
| C.N=72.8N,f=0N | D.N=77N,f=4N |
2013年12月2日晚,发射了嫦娥三号。几天后,运载火箭将嫦娥三号直接送入地月转移轨道;近月制动被月球捕获,进入距月球表面高h环月圆轨道。作为地球天然卫星的月球,月球的质量M,已知月球直径约为r,则月球的平均密度ρ和圆轨道的运行周期T。(引力常量为G)
A. ; ; |
B.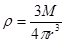 ; ;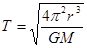 |
C.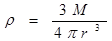 ; ; |
D. ; ;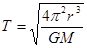 |
在如图所示的xoy,平面直角坐标系中,一足够长绝缘薄板正好和x轴的正半轴重合,在y>a和y<-a的区域内均分布着方向垂直纸面向里的相同的匀强磁场。一带正电粒子,从y轴上的(0,a)点以速度v沿与y轴负向成45°角出射。带电粒子与挡板碰撞前后,x方向的分速度不变,y方向的分速度反向、大小不变。已知粒子质量为m,电荷量为q,磁感应强度的大小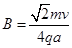 。不计粒子的重力。
。不计粒子的重力。
(1)求粒子进入下方磁场后第一次打在绝缘板上的位置
(2)若在绝缘板上的合适位置开一小孔,粒子穿过后能再次回到出发点。写出在板上开这一小孔可能的位置坐标(不需要写出过程)
(3)在满足(2)的情况下,求粒子从出射到再次返回出发点的时间
如图所示,在绝缘水平面上固定着一光滑绝缘的圆形槽,在某一过直径的直线上有O、 A、D、B四点,其中O为圆心,D在圆上,半径OC垂直于OB。A点固定电荷量为Q的正电荷,B点固定一个未知电荷,使得圆周上各点电势相等。有一个质量为m,电荷量为-q的带电小球在滑槽中运动,在C点受的电场力指向圆心,根据题干和图示信息可知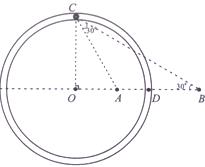
A.固定在B点的电荷带正电
B.固定在B点的电荷电荷量为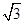 Q
Q
C.小球在滑槽内做匀速圆周运动
D.C、D两点的电场强度大小相等
如图所示,一条质量分布均匀的长度为L的铁链置于光滑水平桌面上.用手按着一端,使另一端长L0的一段下垂.放开手后使铁链从静止开始下滑,当铁链完全通过桌边的瞬间时,铁链具有的速率为

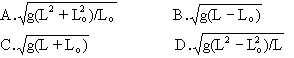
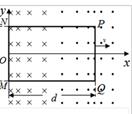
如图甲所示,在真空中,半径为R的圆形区域内存在匀强磁场,磁场方向垂直纸面向外。在磁场左侧有一对平行金属板M、N,两板间距离也为R,板长为L,板的中心线O1O2与磁场的圆心O在同一直线上。置于O1处的粒子发射源可连续以速度v0沿两板的中线O1O2发射电荷量为q、质量为m的带正电的粒子(不计粒子重力),MN两板不加电压时,粒子经磁场偏转后恰好从圆心O的正下方P点离开磁场;若在M、N板间加如图乙所示交变电压UMN,交变电压的周期为 ,t=0时刻入射的粒子恰好贴着N板右侧射出。求
,t=0时刻入射的粒子恰好贴着N板右侧射出。求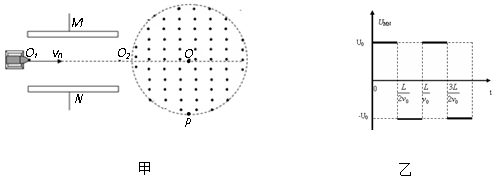
(1)匀强磁场的磁感应强度B的大小
(2)交变电压电压U0的值
(3)若粒子在磁场中运动的最长、最短时间分别为t1、t 2 ,则它们的差值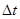 为多大?
为多大?
现代宇宙学认为,恒星在演变过程中,有可能形成密度很大的天体,即成为白矮星或中子星。已知某中子星的密度为1.4×1017kg/m3。求绕该中子星做匀速圆周运动的卫星的最小周期T。
计算结果取一位有效数字,已知引力常量G=6.67×10-11N·m2/kg2。
为了科学研究的需要,常常将质子(带有一个正的元电荷,质量为一个原子质量单位)和α粒子(带有两个正的元电荷,质量为四个原子质量单位)等带电粒子贮存在圆环状空腔中,圆环状空腔置于一个与圆环平面垂直的匀强磁场中,带电粒子在其中做匀速圆周运动(如图)。如果质子和α粒子分别在两个完全相同的圆环状空腔中做圆周运动,且在同样的匀强磁场中,比较质子和α粒子在圆环状空腔中运动的动能EH和Eα,运动的周期TH和Tα的大小,有
| A.EH=Eα,TH=Tα | B.EH=Eα,TH≠Tα |
| C.EH≠Eα,TH=Tα | D.EH≠Eα,TH≠Tα |
减速带是交叉路口上常见的一种交通设施,在某小区门口有一橡胶减速带(如图),有一警用巡逻车正以最大速度20m/s从小区门口经过,在离减速带50m时警察发现一逃犯正以10m/s的速度骑电动车匀速通过减速带,而巡逻车要匀减速到5m/s通过减速带(减速带的宽度忽略不计),减速到5m/s后立即以2.5m/s2的加速度继续追赶,设在整个过程中,巡逻车与逃犯均在水平直道上运动,求从警察发现逃犯到追上逃犯需要的时间。
正对着并水平放置的两平行金属板连接在如图电路中,两板间有垂直纸面磁感应强度为B的匀强磁场,D为理想二极管(即正向电阻为0,反向电阻无穷大),R为滑动变阻器,R0为定值电阻。将滑片P置于滑动变阻器正中间,闭合电键S,让一带电质点从两板左端连线的中点N以水平速度v0射入板间,质点沿直线运动。在保持电键S闭合的情况下,下列说法正确的是( )
| A.质点可能带正电,也可能带负电 |
| B.若仅将滑片P向上滑动一段后,再让该质点从N点以水平速度v0射入板间,质点运动轨迹一定会向上偏 |
| C.若仅将滑片P向下滑动一段后,再让该质点从N点以水平速度v0射入板间,质点依然会沿直线运动 |
| D.若仅将两平行板的间距变大一些,再让该质点从N点以水平速度v0射入板间,质点运动轨迹会向下偏 |
在如图所示的直角坐标系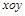 中,矩形区域
中,矩形区域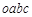 内有垂直于纸面向外的匀强磁场,磁感应强度大小为B=5.0×10-2T;第一象限内有沿
内有垂直于纸面向外的匀强磁场,磁感应强度大小为B=5.0×10-2T;第一象限内有沿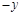 方向的匀强电场,电场强度大小为
方向的匀强电场,电场强度大小为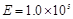 N/C。已知矩形区域
N/C。已知矩形区域 边长为0.06m,ab边长为0.20m。在
边长为0.06m,ab边长为0.20m。在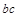 边中点
边中点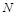 处有一放射源,某时刻,放射源沿纸面向磁场中各方向均匀地辐射出速率均为
处有一放射源,某时刻,放射源沿纸面向磁场中各方向均匀地辐射出速率均为 m/s的某种带正电粒子,带电粒子质量
m/s的某种带正电粒子,带电粒子质量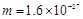 kg,电荷量
kg,电荷量 kg,不计粒子重力,求:(计算结果保留两位有效数字)
kg,不计粒子重力,求:(计算结果保留两位有效数字)
(1)粒子在磁场中运动的半径;
(2)从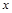 轴上射出的粒子中,在磁场中运动的最短路程为多少?
轴上射出的粒子中,在磁场中运动的最短路程为多少?
(3)放射源沿-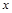 方向射出的粒子,从射出到从
方向射出的粒子,从射出到从 轴离开所用的时间。
轴离开所用的时间。
如图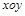 平面为光滑水平面,现有一长为
平面为光滑水平面,现有一长为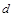 宽为
宽为 的线框
的线框 在外力
在外力 作用下,沿正
作用下,沿正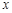 轴方向以速度
轴方向以速度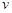 做匀速直线运动,空间存在竖直方向的磁场,磁感应强度
做匀速直线运动,空间存在竖直方向的磁场,磁感应强度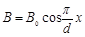 (式中
(式中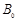 为已知量),规定竖直向下方向为磁感应强度正方向,线框电阻为
为已知量),规定竖直向下方向为磁感应强度正方向,线框电阻为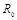 ,
, 时刻
时刻 边恰好在
边恰好在 轴处,则下列说法正确的是( )
轴处,则下列说法正确的是( )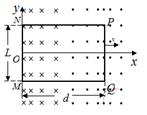
A.外力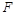 为恒力 为恒力 |
B.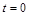 时,外力大小 时,外力大小 |
C.通过线圈的瞬时电流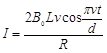 |
D.经过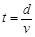 ,线圈中产生的电热 ,线圈中产生的电热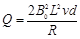 |
如图所示,固定的光滑平台左端固定有一光滑的半圆轨道,轨道半径为R,平台上静止放着两个滑块A、B,其质量mA=m,mB =2m,两滑块间夹有少量炸药.平台右侧有一小车,静止在光滑的水平地面上,小车质量M=3m,车长L=2R,车面与平台的台面等高,车面粗糙,动摩擦因数μ=0.2,右侧地面上有一立桩,立桩与小车右端的距离为S,S在0<S<2R的范围内取值,当小车运动到立桩处立即被牢固粘连。点燃炸药后,滑块A恰好能够通过半圆轨道的最高点D,滑块B冲上小车.两滑块都可以看作质点,炸药的质量忽略不计,爆炸的时间极短,爆炸后两个滑块的速度方向在同一水平直线上,重力加速度为g=10m/s2.求:
(1)滑块A在半圆轨道最低点C受到轨道的支持力FN。
(2)炸药爆炸后滑块B的速度大小vB。
(3)请讨论滑块B从滑上小车在小车上运动的过程中,克服摩擦力做的功Wf与S的关系。