高中数学组合几何选择题

设函数的导函数为，对任意R都有成立，则（   ）

A．

B．

C．

D．的大小不确定

已知函数是函数的导函数，则的图象大致是（  ）

若曲线f(x，y)＝0上两个不同点处的切线重合，则称这条切线为曲线f(x，y)＝0的“自公切线”．下列方程：①x²－y²＝1；②y＝x²－|x|；③y＝3sin x＋4cos x；④|x|＋1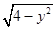＝对应的曲线中存在“自公切线”的有 （  ）

A．①②

B．②③

C．①④

D．③④

曲线在点处的切线与坐标轴所围三角形的面积为 （   ）

A．

B．

C．

D．

曲线（其中e＝2.71828…是自然对数的底数）在点处的切线的斜率为（  ）

A．2

B．3

C．

D．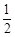

曲线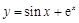（其中e＝2.71828…是自然对数的底数）在点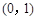处的切线的斜率为（ ）

A．2

B．3

C．

D．

过曲线C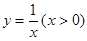：上一点作曲线C的切线，若切线的斜率为－4，则等于（   ）

A．2

B．

C．4

D．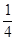

曲线y=x³﹣2x+4在点（1，3）处的切线的倾斜角为

A．30°

B．45°

C．60°

D．120°

已知直线与曲线相切，则

A．-1

B．-2

C．0

D．2

曲线在点处的切线方程是(    )

A．

B．

C．

D．

函数在点处的切线斜率的最小值是（   ）

A．

B．

C．

D．

已知函数，是的导数，的大致图象是（  ）

是函数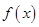的导数，函数是增函数（是自然对数的底数），与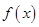的大小关系是（  ）

A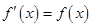．	B．
C．	D．

函数在点处的切线方程是（  ）

A．

B．

C．

D．

如图，直线是曲线在处的切线，则（   ）

A．

B．3

C．4

D．5