函数 的定义域为A,若
的定义域为A,若 且
且 时总有
时总有 ,则称
,则称 为单函数.例如,函数
为单函数.例如,函数 是单函数.下列命题:
是单函数.下列命题:
①函数 是单函数;
是单函数;
②若 为单函数,
为单函数, 且
且 则
则 ;
;
③若f:A B为单函数,则对于任意b
B为单函数,则对于任意b B,它至多有一个原象;
B,它至多有一个原象;
④函数 在某区间上具有单调性,则
在某区间上具有单调性,则 一定是该区间上的单函数.
一定是该区间上的单函数.
其中的真命题是 .(写出所有真命题的编号)
已知定义在 上的
上的 为奇函数,且在区间
为奇函数,且在区间 上单调递增,则满足
上单调递增,则满足 的
的 的取值范围为____ ▲ __
的取值范围为____ ▲ __
如图所示,动物园要围成四间相同面积的长方形虎笼,一面可利用原有的墙,其它各面用钢筋网围成。现有36m长的钢筋网材料,则可围成的每间虎笼面积最大为_________m2。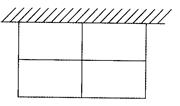
集合M={f(x)|存在实数t使得函数f(x)满足f(t+1)=f(t)+f(1)},则下列函数(a、b、c、k都是常数):
① y=kx+b(k≠0,b≠0);② y=ax2+bx+c(a≠0);
③ y=ax(0<a<1);④ y= (k≠0);⑤ y=sinx.
(k≠0);⑤ y=sinx.
其中属于集合M的函数是________.(填序号)