高中数学几何中的变换：对称、平移、旋转试题

设O为坐标原点，F为抛物线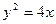的焦点，A是抛物线上一点，若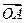·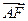=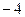，则点A的坐标是                      （    ）

A．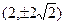

B．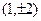

C．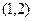

D．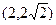

将函数进行平移，使得到的图形与抛物线的两个交点关于原点对称，试求平移后的图形对应的函数解析式．

将函数的图象F按向量平移后所得到的图象的解析式是，求向量．

已知图形F上的点A按向量平移前后的坐标分别是和，若B（）是图形F上的又一点，则在F按向量平移后得到的图形F^，上B^，的坐标是（   ）

A．	B．
C．	D．

将函数="2x" +1的图像按向量平移得函数=的图像则
A =（ 1） B =（1 ，1） C =()   D (1 ，1）

向量，，，为了得到函数的图象，可将函数的图象         （   ）

A．向右平移个单位长度	B．向右平移个单位长度
C．向左平移个单位长度	D．向左平移个单位长度

若将函数的图象按向量a平移，使图上点P的坐标由（1，0）变为（2，2），则平移后图象的解析式为

A．	B．
C．	D．

要得到函数的图象，只需要把函数的图象（  ）

A．向左平移2个单位	B．向右平移2个单位
C．向左平移6个单位	D．向右平移6个单位

把函数的图像按向量平移，得到的图像，则（    ）

A．

B．-3

C．

D．-3

将的图象按向量平移，则平移后所得图象的解析式为（　　）

A．	B．
C．	D．

将函数的图象按向量平移所得的图象关于轴对称，则最小正值是                                                                 （   ）

A．

B．

C．

D．

把函数y=4^x的图象按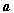平移到F′, F′的函数解析式为y=4^x-2-2, 则向量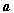的坐标等于_____

函数 $y=\cos \left(2x+\frac{\mathrm{\pi }}{6}\right)-2$的图像 $F$按向量 $\mathit{a}$平移到 $F`$， $F`$的解析式 $y=f\left(x\right)$，当 $y=f\left(x\right)$为奇函数时，向量 $\mathit{a}$可以等于（）

A．

$\left(\frac{\mathrm{\pi }}{6},-2\right)$

B．

$\left(\frac{\mathrm{\pi }}{6},2\right)$

C．

$\left(-\frac{\mathrm{\pi }}{6},-2\right)$

D．

$\left(-\frac{\mathrm{\pi }}{6},2\right)$

已知向量＝(1，1)向量与向量夹角为，且·＝－1.则向量＝______．

设0≤θ≤2π时，已知两个向量＝(cosθ，sinθ)，＝(2＋sinθ，2－cosθ)，则向量长度的最大值是                                                                     （   ）

A．

B．

C．3

D．2