高中数学函数迭代选择题

二次函数f(x)＝ax²＋bx＋c对一切x∈R，满足f(1－x)＝f(1＋x)，且f(－1)<0，f(0)>0，则(　)

A．a＋b＋c<0

B．b<a＋c

C．c<2b

D．a，b，c均大于0

客车从甲地以60km/h的速度行驶1小时到达乙地，在乙地停留了半小时，然后以80km/h的速度行驶1小时到达丙地.下列描述客车从甲地出发，经过乙地，最后到达丙地所经过的路程s与时间t之间的关系图象中，正确的是

已知是偶函数，而是奇函数，且对任意，
都有，则的大小关系是

A．

B．

C．

D．

若函数则等于 

A．

B．

C．

D．

已知集合，定义函数。若点、、，的外接圆圆心为，且，则满足条件的函数有(   )

A．6个

B．10个

C．12个

D．16个

函数 $f\left(x\right)=x^3+\sin x+1(x\in R)$ ，若 $f\left(a\right)=2$ ,则 $f(-a)$ 的值为

A．

3

B．

0

C．

-1

D．

-2

若函数f (x) =" (sinx" +1)(2a – sinx - 1)的最大值为，则a的取值范围是 (     )

A．R

B．（2，+∞）

C．[0，2]

D．（-∞，0）

设函数，其中表示不超过的最大整数，如，若有三个不同的根，则实数的取值范围是（ ）

A．

B．

C．

D．

函数a在上恒成立，则a的取值范围是【  】.

A．

B．

C．

D．

设，则等于

A．

B．

C．

D．

函数，的反函数是【   】.

A．	B．
C．	D．

定义，已知实数x，y满足|x|≤2，|y|≤2，
设 则z的取值范围是                                                         （  ）

A．[－7，10]

B．[－6，10]

C．[－6，8]

D．[－7，8]

若关于x的方程有两个不等实根，则的取值范围是     （）

A．

B．

C．

D．

幂指函数在求导时，可运用对数法：在函数解析式两边求对数得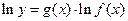，两边同时求导得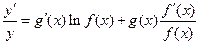，于是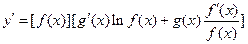．运用此方法可以探求的一个单调递增区间是（   ）

A．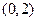

B．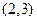

C．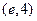

D．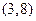

已知对于任意实数，函数满足.若方程有2009个实数解，则这2009个实数解之和为
A  0   B 1   C   D 2