已知函数f(x)的定义域为(﹣∞,0)∪(0,+∞),f(x)是奇函数,且当x>0时,f(x)=x2﹣x+a,若函数g(x)=f(x)﹣x的零点恰有两个,则实数a的取值范围是( )
| A.a<0 | B.a≤0 | C.a≤1 | D.a≤0或a=1 |
若曲线C1:x2+y2﹣2x=0与曲线C2:y(y﹣mx﹣m)=0有四个不同的交点,则实数m的取值范围是( )
A.(﹣ , , ) ) |
B.(﹣ ,0)∪(0, ,0)∪(0, ) ) |
C.[﹣ , , ] ] |
D.(﹣∞,﹣ )∪( )∪( ,+∞) ,+∞) |
已知函数 与
与 的图像在
的图像在 上不间断,由下表知方程f(x)=g(x)有实数解的区
上不间断,由下表知方程f(x)=g(x)有实数解的区
间是( )
| x |
-1 |
0 |
1 |
2 |
3 |
| f(x) |
-0.677 |
3.011 |
5.432 |
5.980 |
7.651 |
| g(x) |
-0.530 |
3.451 |
4.890 |
5.241 |
6.892 |
A.(-1,0) B.(0,1) C.(1,2) D.(2,3)
关于 的方程
的方程 ,给出下列四个命题:
,给出下列四个命题:
①存在实数 ,使得方程恰有2个不同的实根
,使得方程恰有2个不同的实根
②存在实数 ,使得方程恰有4个不同的实根
,使得方程恰有4个不同的实根
③存在实数 ,使得方程恰有5个不同的实根
,使得方程恰有5个不同的实根
④存在实数 ,使得方程恰有8个不同的实根
,使得方程恰有8个不同的实根
其中假命题的个数是( )
| A.0 | B.1 | C.2 | D.3 |
已知定义在R上的函数 的对称轴为
的对称轴为 ,且当
,且当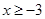 时,
时, ,若函数
,若函数 在区间
在区间
 上有零点,则k的值为( )
上有零点,则k的值为( )
| A.2或-7 | B.2或-8 | C.1或-7 | D.1或-8 |