高中数学随机思想的发展选择题

设随机变量∽∽，记，则

A．

B．

C．

D．的大小关系不定

在篮球比赛中，罚球命中1次得1分，不中得0分，如果运动员甲罚球命中的概率是0.8，记运动员甲罚球1次的得分为，则等于（）

A．0.2

B．0.4

C．0.8

D．1

已知随机变量的值等于
（）

A．0.5

B．0.2

C．0.3

D．0.4

已知随机变量，若，则等于( )

A．

B．

C．

D．

设一随机试验的结果只有A和，，令随机变量，
则X的方差为( )

A．

B．

C．

D．

抛掷两枚骰子,当至少有一枚5点或一枚6点出现时,就说这次实验成功,则在30次实验中成功次数的期望是

A．

B．

C．

D．10

抛掷两枚骰子，当这两枚骰子都出现大数（4点或大于4点）时，就认为试验成功。则在30次试验中成功次数的数学期望与方差分别为（）

A．

B．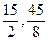

C．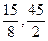

D．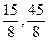

①某机场候机室中一天的游客数量为X②某网站一天的点击数X
③某水电站观察到一天中水位X
其中是离散型随机变量的是

A．①②中的X

B．①③中的X

C．②③中的X

D．①②③中的X

甲、乙、丙三名射箭运动员在某次测试中各射箭12次，三人的测试成绩如下表

甲的成绩
环数	7	8	9	10
频数	3	3	3	3

乙的成绩
环数	7	8	9	10
频数	4	2	2	4

丙的成绩
环数	7	8	9	10
频数	2	4	4	2

分别表示甲、乙、丙三名运动员这次测试成绩的标准差，则有（　　）

A．

B．

C．

D．

某事件A发生的概率为，则事件A在一次试验中发生的次数的方差的最大值为（）

A．

B．

C．

D．

设随机变量服从B（6，），则P（=3）的值是（）

A．

B．

C．

D．

某篮球运动员罚球命中率为0.8，命中得1分，没有命中得0分，则他罚球1次的得分X的方差为（）

A．0.18

B．0.20

C．0.14

D．0.16

下列说法中正确的是

A．离散型随机变量ξ的期望Eξ反映了ξ的值的概率的平均值

B．离散型随机变量ξ的方差Dξ反映了ξ取值的平均水平

C．离散型随机变量ξ的期望Eξ反映了ξ取值的平均水平

D．离散型随机变量ξ的方差Dξ反映了ξ取值的概率的平均值

如果是离散型随机变量，，那么（　　）

A．，	B．，
C．，	D．，

某种种子每粒发芽的概率都为0.9，现播种了1000粒，对于没有发芽的种子，每粒需再补种2粒，补种的种子数记为 $X$，则 $X$的数学期望为（ ）.

A．

100

B．

200

C．

300

D．

400