高中数学正交试验设计方法试题

为考察某种药物预防禽流感的效果，进行动物家禽试验，调查了100个样本，统计结果为：服用药的共有60个样本，服用药但患病的仍有20个样本，没有服用药且未患病的有20个样本.
（1）根据所给样本数据完成下面2×2列联表；
（2）请问能有多大把握认为药物有效？

	不得禽流感	得禽流感	总计
服药
不服药
总计

 

某班主任对全班50名学生进行了作业量多少的调查，数据如下表：

	认为作业多	认为作业不多	总数
喜欢玩电脑游戏	18	9	27
不喜欢玩电脑游戏	8	15	23
总数	26	24	50

根据表中数据得到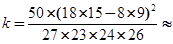5.059，因为p(K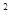≥5.024)=0.025,
则认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约为（ ）
(A)97.5%     (B) 95%       (C)90%        (D)无充分根据

为了解某班关注NBA（美国职业篮球）是否与性别有关，对某班48人进行了问卷调查得到如下的列联表：

	关注NBA	不关注NBA	合计
男生		6
女生	10
合计			48

 
已知在全班48人中随机抽取1人，抽到关注NBA的学生的概率为.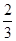
（1）请将上面的表补充完整（不用写计算过程），并判断是否有95%的把握认为关注NBA与性别有关？说明你的理由；
（2）设甲，乙是不关注NBA的6名男生中的两人，丙，丁，戊是关注NBA的10名女生中的3人，从这5人中选取2人进行调查，求：甲，乙至少有一人被选中的概率.
答题参考

P（K^2≥k）	0.10	0.05	0.010	0.005
k0	2.706	3.841	6.635	7.879

 

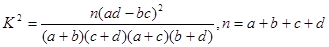
设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别是0.6，0.5,0.5,0.4，各人是否使用设备相互独立，
（1）求同一工作日至少3人需使用设备的概率；
(2)实验室计划购买台设备供甲、乙、丙、丁使用，若要求"同一工作日需使用设备的人数大于的概率小于0.1，求的最小值.

一款击鼓小游戏的规则如下：每盘游戏都需要击鼓三次，每次击鼓要么出现一次音乐，要么不出现音乐；每盘游戏击鼓三次后，出现一次音乐获得10分，出现两次音乐获得20分，出现三次音乐获得100分，没有出现音乐则扣除200分（即获得-200分）.设每次击鼓出现音乐的概率为，且各次击鼓出现音乐相互独立.
（1）设每盘游戏获得的分数为，求的分布列；
（2）玩三盘游戏，至少有一盘出现音乐的概率是多少？
（3）玩过这款游戏的许多人都发现，若干盘游戏后，与最初的分数相比，分数没有增加反而减少了.请运用概率统计的相关知识分析分数减少的原因.

乒乓球台面被球网分成甲、乙两部分，如图，
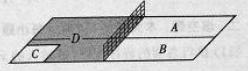甲上有两个不相交的区域，乙被划分为两个不相交的区域.某次测试要求队员接到落点在甲上的来球后向乙回球.规定：回球一次，落点在上记3分，在上记1分，其它情况记0分.对落点在上的来球，队员小明回球的落点在上的概率为，在上的概率为；对落点在上的来球，小明回球的落点在上的概率为，在上的概率为.假设共有两次来球且落在上各一次，小明的两次回球互不影响.求：
（Ⅰ）小明的两次回球的落点中恰有一次的落点在乙上的概率；
（Ⅱ）两次回球结束后，小明得分之和的分布列与数学期望.

随机观测生产某种零件的某工厂名工人的日加工零件数（单位：件），获得数据如下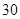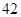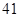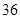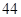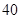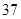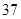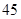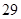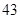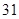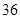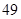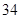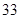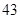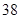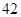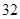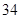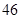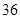：、、、、、、、、、、、、、、、、、、、、、、、、，根据上述数据得到样本的频率分布表如下：

分组	频数	频率

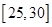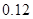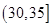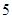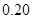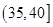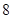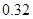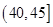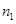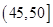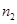（1）确定样本频率分布表中的值；
（2）根据上述频率分布表，画出样本频率分布直方图；
（3）根据样本频率分布直方图，求在该厂任取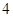人，至少有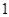人的日加工零件数落在区间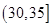的概率.

设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别为各人是否需使用设备相互独立.
（1）求同一工作日至少3人需使用设备的概率；
（2）表示同一工作日需使用设备的人数，求的数学期望.

某中学将100名高一新生分成水平相同的甲、乙两个“平行班”，每班50人．陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验．为了了解教学效果，期末考试后，陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计，作出茎叶图如下．记成绩不低于90分者为“成绩优秀”．

甲		乙
6	9	3 6 7 9 9
9 5 1 0	8	0 1 5 6
9 9 4 4 2	7	3 4 5 8 8 8
8 8 5 1 1 0	6	0 7 7
4 3 3 2	5	2 5

 
(1)在乙班样本中的20个个体中，从不低于86分的成绩中随机抽取2个，求抽出的两个均“成绩优秀”的概率；
(2)由以上统计数据填写下面列联表，并判断是否有90%的把握认为：“成绩优秀”与教学方式有关.

	甲班(A方式)	乙班(B方式)	总计
成绩优秀
成绩不优秀
总计

 
附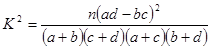：,其中n＝a＋b＋c＋d.)

P(K^2≥k)	0.25	0.15	0.10	0.05	0.025	0.01	0.005	0.001
k	1.323	2.072	2.706	3.841	5.024	6.635	7.879	10.828

 

在吸烟与患肺病这两个分类变量的计算中，下列说法正确的是(　　)
①若K²的观测值满足K²≥6.635，我们有99%的把握认为吸烟与患肺病有关系，那么在100个吸烟的人中必有99人患有肺病；②从独立性检验可知有99%的把握认为吸烟与患病有关系时，我们说某人吸烟，那么他有99%的可能患有肺病；③从统计量中得知有95%的把握认为吸烟与患肺病有关系，是指有5%的可能性使得推断出现错误

A．①

B．①③

C．③

D．②

甲、乙两人将参加某项测试，他们能达标的概率都是0.8，设随机变量为两人中能达标的人数，则的数学期望为        ．   

老师要从10篇课文中随机抽3篇让学生背诵，规定至少要背出其中2篇才能及格．某同学只能背诵其中的6篇，试求：
(1)抽到他能背诵的课文的数量的分布列；
(2)他能及格的概率．

如图，从A₁(1，0，0)、A₂(2，0，0)、B₁(0，1，0)、B₂(0，2，0)、C₁(0，0，1)、C₂(0，0，2)这6个点中随机选取3个点，将这3个点及原点O两两相连构成一个“立体”，记该“立体”的体积为随机变量V(如果选取的3个点与原点在同一个平面内，此时“立体”的体积V＝0)．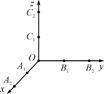

(1)求V＝0的概率；
(2)求V的分布列及数学期望E(V)．

设50件商品中有15件一等品，其余为二等品．现从中随机选购2件，则所购2件商品中恰有一件一等品的概率为________．

某校150名教职工中，有老年人20个，中年人50个，青年人80个，从中抽取20个作为样本．
①采用随机抽样法：抽签取出30个样本；
②采用系统抽样法：将教工编号为00,01，…，149，然后平均分组抽取30个样本；
③采用分层抽样法：从老年人，中年人，青年人中抽取30个样本．
下列说法中正确的是(　　)

A．无论采用哪种方法，这150个教工中每一个被抽到的概率都相等

B．①②两种抽样方法，这150个教工中每一个被抽到的概率都相等；③并非如此

C．①③两种抽样方法，这150个教工中每一个被抽到的概率都相等；②并非如此

D．采用不同的抽样方法，这150个教工中每一个被抽到的概率是各不相同的