高中数学误差估计填空题

下图是某高三学生进入高中三年来第次到次的数学考试成绩茎叶图，根据茎叶图计算数据的中位数为         .

甲、乙两名运动员在某项测试中的6次成绩如茎叶图所示, 分别表示甲、乙两名运动员这项测试成绩的平均数, 分别表示甲、乙两名运动员这项测试成绩的标准差,则有（ 　　）

A．,	B．,
C．,	D．,

某地区对某段公路上行驶的汽车速度监控,从中抽取200辆汽车进行测速分析,得到如图所示的频率分布直方图,根据该图,可估计这组数据的平均数和中位数依次为          .

某地区对某段公路上行驶的汽车速度监控,从中抽取200辆汽车进行测速分析,得到如图所示的频率分布直方图,根据该图,可估计这组数据的平均数和中位数依次为          .

从某地高中男生中随机抽取100名同学，将他们的体重（单位：kg）数据绘制成频率分布直方图（如图）．由图中数据可知体重的平均值为　　　kg；若要从体重在[ 60 , 70），[70 ，80) , [80 , 90]三组内的男生中，用分层抽样的方法选取12人参加一项活动，再从这12人选两人当正负队长，则这两人身高不在同一组内的概率为        ． 

某小学对学生的身高进行抽样调查，如图，是将他们的身高（单位：厘米）数据绘制的频率分布直方图．若要从身高在［120，130），［130，140），［140，150］三组内的学生中，用分层抽样的方法选取18人，则从身高在［140，150］内的学生中选取的人数应为________.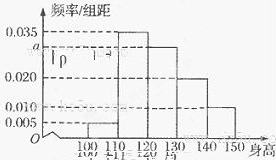

如图是甲、乙两名篮球运动员2012年赛季每场比赛得分的茎叶图，则甲、乙两人比赛得分的中位数之和是______.

以下茎叶图记录了甲、乙两组各四名工人天加工的零件数，则甲组工人天每人加工零件的平均数为____________；若分别从甲、乙两组中随机选取一名工人，则这两名工人加工零件的总数超过了的概率为________

某校高中年级开设了丰富多彩的校本课程，甲、乙两班各随机抽取了5名学生的学分，用茎叶图表示如图，则甲、乙两班抽取的5名学生学分的中位数的和等于      。

某校为了解高一学生寒假期间学习情况，抽查了100名同学，统计他们每天平均
学习时间，绘成频率分布直方图（如图）．

则这100名同学中学习时间在6至8小时之间的人数为     ．

某试验对象的取值范围是区间内的整数，现采用分数法进行优选，则第一个试点值可以是        。

为了调查甲、乙两个网站受欢迎的程度，随机选取了14天，统计上午8：00—10：00间各自的点击量，得如下所示的统计图，根据统计图：
（1）甲、乙两个网站点击量的极差分别是多少？  
（2）甲网站点击量在[10，40]间的频率是多少？  
（3）甲、乙两个网站哪个更受欢迎？并说明理由。

已知辆汽车通过某一段公路时的时速的频率分布直方图如右图所示，求时速在的汽车大约有__▲__辆.

	频率

 

某企业三月中旬生产，A、B、C三种产品共3000件，根据分层抽样的结果；企
业统计员制作了如下的统计表格：

由于不小心，表格中A、C产品的有关数据已被污染看不清楚，统计员记得A产品的样本容量比C产品的样本容量多10，根据以上信息，可得C的产品数量是          件。

某校为了了解高三同学暑假期间学习情况，调查了200名同学，统计他们每天平均学习时间，绘成频率分布直方图（如图）。则这200名同学中学习时间在6～8小时的同学为_______________人；