高中数学误差估计选择题

一组数据共有7个数，记得其中有10,2,5,2,4,2，还有一个数没记清，但知道这组数的平均数、中位数、众数依次成等比数列，这个数的所有可能值的和为

A．9

B．3

C．20

D．-11

在刚召开的十二届全国人大一次会上，为了调查人大代表对“反腐倡廉”的意见，现从1000
名代表中使用系统抽样，按以下规定获取样本编号：如果在起始组中随机抽取的号码为M ，那么第K组（组
号K从0开始，K=0,1,2，，9）抽取的号码的百位数为组号，后两位数为M+32K的后两位数，若M=16，
则时所抽取的样本编号为（   ）

A．444 ，740

B．416，716

C．444，726

D．423，726

在某次测量中得到的A样本数据如下：82,84,84,86,86,86,88,88,88,88.若B样本数据 恰好是A样本数据都加2后所得数据，则A，B两样本的下列数字特征对应相同的是

A．众数

B．平均数

C．中位数

D．标准差

如图所示，图中有5组数据，去掉　　　组数据后（填字母代号），剩下的4组数据的线性相关性最强（     ）

A．

B．

C．

D．

从甲乙两个城市分别随机抽取16台自动售货机，对其销售额进行统计，统计数据用茎叶图表示（如图所示），设甲乙两组数据的平均数分别为，，中位数分别为，，则（    ）

A．，

B．，

C．，

D．，

一个车间为了规定工时定额，需要确定加工零件所花费的时间，为此进行了8次试验，收集数据如下：

零件个数x（个）	10	20	30	40	50	60	70	80
加工时间y（分钟）	62	68	75	81	89	95	102	108

设回归直线方程为，则点在直线的（   ）
A、右上方       B、右下方       C、左上方       D、左下方

一批产品抽50件测试，其净重介于13克与19克之间，将测试结果按如下方式分成六组：第一组，净重大于等于13克且小于14克；第二组，净重大于等于14克且小于15克；         第六组，净重大于等于18克且小于19克．如图是按上述分组方法得到的频率分布直方图．设净重小于17克的产品数占抽取数的百分比为，净重大于等于15克且小于17克的产品数为，则从频率分布直方图中可分析出和分别为(    )

A．	B．
C．	D．

某班50名学生其中考试数学成绩的频率分布直方图如图所示.其中成绩分组区间是：，， ，，.则图中的值为（     ）

A．0.18

B．0.018

C．0.36

D．0.009

在如图所示的“茎叶图”表示的数据中，众数和中位数分别（　 ）.

Ａ．23与26　 B．31与26    C．24与30　 D．26与30

统计某校1000名学生的数学水平测试成绩，得到样本频率分布直方图如图所示，若满分为100分，规定不低于60分为及格，则及格率是

A．20%

B．25%

C．6%

D．80%

某校从参加高二年级学业水平测试的学生中抽出100名学生，其数学成绩的频率分布直方图如图所示．其中 成绩分组区间是[40，50），[50,60），[60,70），[70,80），  [80,90) ,[90,100]．则成绩在[80 ,100]上的人数为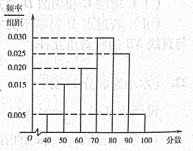

A．70

B．60

C．35

D．30

一个样本a,3,5,7的平均数是b，且a、b是方程x²－5x＋4＝0的两根，则这个样本的方差是(　　)

A．3

B．4

C．5

D．6

有一个容量为66的样本，数据的分组及各组的频数如下：
[11．5，15．5）  2  [15．5,19．5） 4  [19．5，23．5） 9 [23．5,27．5） 18
[27．5，31．5）  1l  [31．5，35．5）  12  [35．5．39．5） 7 [39．5,43．5） 3
根据样本的频率分布估计，数据落在[31．5，43．5）的概率约是

A．

B．

C．

D．

对某商店一个月内(按30天计)每天的顾客人数进行了统计,得到样本的茎叶图(如图所示),则该样本的中位数、众数、极差分别是（   ）

A．47,45,56	B．46,45,53
C．46,45,56	D．45,47,53

如图是2012年某校元旦晚会举办的挑战主持人大赛上，七位评委为某选手打出的分数的茎叶统计图，去掉一个最高分和一个最低分后，所剩数据的众数和中位数分别为（　　

A．，	B．，
C．，	D．，