如果反比例函数 的图象经过点(-1,-2),则k的值是( )
的图象经过点(-1,-2),则k的值是( )
| A.2 | B.-2 | C.-3 | D.3 |
如图,已知:在边长为12的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上.若BF=3,则BE长为( )
A.1 B.2.5 C.2.25 D.1.5
如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点D,E,F分别是边AB,BC,AC的中点,连接DE、DF,动点P,Q分别从点A、B同时出发,运动速度均为1cm/s,点P沿AFD的方向运动到点D停止;点Q沿BC的方向运动,当点P停止运动时,点Q也停止运动.在运动过程中,过点Q作BC的垂线交AB于点M,以点P,M,Q为顶点作平行四边形PMQN.设平行四边形边形PMQN与矩形FDEC重叠部分的面积为y(cm2)(这里规定线段是面积为0的几何图形),点P运动的时间为x(s)
(1)当点P运动到点F时,CQ= cm;
(2)在点P从点F运动到点D的过程中,某一时刻,点P落在MQ上,求此时BQ的长度;
(3)当点P在线段FD上运动时,求y与x之间的函数关系式.
某校数学课题学习小组在“测量教学楼高度”的活动中,设计了以下两种方案:
| 课题 |
测量教学楼高度 |
|
| 方案 |
一 |
二 |
| 图示 |
 |
 |
| 测得数据 |
CD=6.9m,∠ACG=22°,∠BCG=13°, |
EF=10m,∠AEB=32°,∠AFB=43° |
| 参考数据 |
sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin13°≈0.22,cos13°≈0.97,tan13°≈0.23 |
sin32°≈0.53,cos32°≈0.85,tan32°≈0.62 sin43°≈0.68,cos43°≈0.73,tan43°≈0.93 |
请你选择其中的一种方法,求教学楼的高度(结果保留整数)
电脑系统中有个“扫雷”游戏,要求游戏者标出所有的雷,游戏规则:一个方块下面最多埋一个雷,如果无雷,掀开方块下面就标有数字,提醒游戏者此数字周围的方块(最多八个)中雷的个数(实际游戏中,0通常省略不标,此WORD中为方便大家识别与印刷,我还是把图乙中的0都标出来吧,以示与未掀开者的区别),如图甲中的“3”表示它的周围八个方块中仅有3个埋有雷.图乙第一行从左数起的七个方块中(方块上标有字母),能够确定一定是雷的有 .(请填入方块上的字母)

有20个同学排成一行,若从左往右隔1人报数,小李报8号;若从右往左隔2人报数,小陈报6号.那么,从小陈开始向小李逐人报数,小李报的号数为( ).
| A.ll | B.12 | C.13 | D.14 |
下列图形中,单独选用一种图形不能进行平面镶嵌的是
| A.正三角形 | B.正六边形 | C.正方形 | D.正五边形 |
认真观察下图的四个图中阴影部分构成的图案,回答下列问题:
(1)利用所学知识,请写出这四个图案都具有的特征: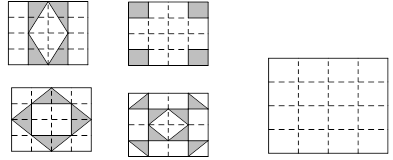
特征1:______________________________________;
特征2:______________________________________;
(2)请在备用图中设计你心目中最美丽的图案,使它也具备你所写的上述
特征.
如图,一个几何体上半部为正四棱椎,下半部为立方体,且有一个面涂有颜色,下列图形中,是该几何体的表面展开图的是
A. |
B. |
C. |
D. |
用半径为10cm,圆心角为216°的扇形做成一个圆锥的侧面,则这个圆锥的高为 cm.
丁丁参加了一次智力竞赛,共回答了30道题,题目的评分标准是这样的:答对一题加5分,一题答错或不答倒扣1分.如果在这次竞赛中丁丁的得分要超过100分,那么他至少要答对多少题?