下图是一数值转换机的示意图,若输入的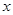 值为20,则输出的结果为( )
值为20,则输出的结果为( )

| A.150 | B.120 | C.60 | D.30 |
某商场销售一种西装和领带,西装每套定价1000元,领带每条定价200元.“国庆节”
期间商场决定开展促销活动,活动期间向客户提供两种优惠方案.
方案一:买一套西装送一条领带;
方案二:西装和领带都按定价的90%付款.
现某客户要到该商场购买西装20套,领带x条(x>20).
(1)若该客户按方案一购买,需付款 元.(用含x的代数式表示)
若该客户按方案二购买,需付款 元.(用含x的代数式表示)
(2)若x=30,通过计算说明此时按(1)哪种方案购买较为合算?
(3)当x=30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法.
如图,长方形的长为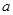 ,宽为
,宽为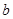 ,
,
(1)用含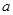 、
、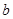 的代数式表示右图阴影部分的面积S阴影.
的代数式表示右图阴影部分的面积S阴影.
(2)当a=5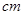 ,b=2
,b=2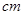 时,求S阴影.(
时,求S阴影.(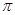 取3.14)
取3.14)
已知: 与
与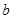 互为相反数,
互为相反数,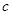 与
与 互为倒数,当
互为倒数,当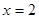 时,求代数式
时,求代数式 的值.
的值.
|
先阅读下面的解题过程,在解答后面的题目.
例:已知式子9-6y-4y2 =7,求2y2 +3y+7的值.已知a,b互为相反数,c,d互为倒数,x的绝对值为5,试求:(a+b+cd)x2+(a+b)2008-(-cd)2015的值.
某餐厅中,一张桌子可坐6人,有以下两种摆放方式:
(1)当有 张桌子时,两种摆放方式各能坐多少人?
张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌,若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌,为什么?