如图,兰兰站在河岸上的G点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,测得小船C的俯角是∠FDC=30°,若兰兰的眼睛与地面的距离是1.5米,BG=1米,BG平行于AC所在的直线,迎水坡的坡度i=4:3,坡长AB=10米,求小船C到岸边的距离CA的长?(参考数据: =1.73,结果保留两位有效数字)
=1.73,结果保留两位有效数字)
计算:
(1)( )-1-3tan60°+
)-1-3tan60°+ ;
;
(2)(a+2)(a-2)-(a-1)2.
已知函数 中自变量的取值范围是( ).
中自变量的取值范围是( ).
A. |
B.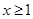 |
C.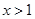 |
D.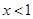 |
直线EF、GH之间有一个直角三角形ABC,其中∠BAC = 90°,∠ABC =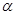 .
.
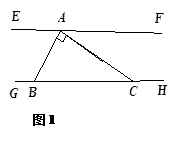
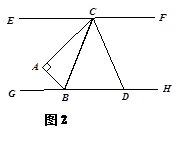
(1)如图1,点A在直线EF上,B、C在直线GH上,若∠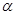 =60°,∠FAC =30°.求证:EF∥GH;
=60°,∠FAC =30°.求证:EF∥GH;
(2)将三角形ABC如图2放置,直线EF∥GH,点C 、B分别在直线EF、GH上,且BC平分∠ABH,直线CD平分∠FCA交直线GH于D.在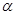 取不同数值时,∠BCD的大小是否发生变化?若不变求其值,若变化指出其变化范围.
取不同数值时,∠BCD的大小是否发生变化?若不变求其值,若变化指出其变化范围.
如图,在△ABC中,AB=AC=15,点D是BC边上的一动点(不与B、C重合),∠ADE=∠B=∠α,DE交AB于点E,且tan∠α= .有以下的结论:
.有以下的结论:
①△ADE∽△ACD;
②当CD=9时,△ACD与△DBE全等;
③△BDE为直角三角形时,BD为12或 ;
;
④0<BE≤ ,
,
其中正确的结论是 (填入正确结论的序号).
某海域有A,B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求该船与B港口之间的距离即CB的长(结果保留根号).
如图,一艘轮船航行到B处时,测得小岛A在船的北偏东60°的方向,轮船从B处继续向正东方向航行200海里到达C处时,测得小岛A在船的北偏东30°的方向.己知在小岛周围170海里内有暗礁,若轮船不改变航向继续向前行驶,试问轮船有无触礁的危险?( ≈1.732)
≈1.732)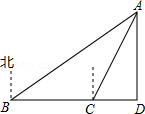
在△ABC中,若角A,B满足 ,则∠C的大小是( )
,则∠C的大小是( )
| A.45° | B.60° | C.75° | D.105° |
如图,从热气球C上测得两建筑物A、B底部的俯角分别为30°和60度.如果这时气球的高度CD为90米.且点A、D、B在同一直线上,求建筑物A、B间的距离.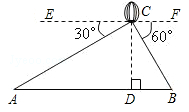
(满分9分)如图,公园入口处原有三级台阶,每级台阶高为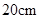 ,深为
,深为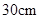 ,为方便残疾人士,拟将台阶改成斜坡,台阶的起点为
,为方便残疾人士,拟将台阶改成斜坡,台阶的起点为 ,斜坡的起始点为
,斜坡的起始点为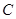 (如图所示),如果斜坡的坡角
(如图所示),如果斜坡的坡角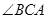 设计为
设计为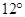 ,那么斜坡起点
,那么斜坡起点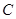 应离
应离 点多远?
点多远?
(精确到 ,参考数据:
,参考数据: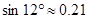 ,
,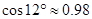 ,
, )
)
(本题8分)如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.
(1)求∠BPQ的度数;
(2)求该电线杆PQ的高度(结果精确到1m).备用数据: ,
,