如图所示,在x轴的上方(y>0的空间内)存在着垂直于纸面向里、磁感应强度为B的匀强磁场,一个不计重力的带正电粒子从坐标原点O处以速度v进入磁场,粒子进入磁场时的速度方向垂直于磁场且与x轴正方向成45°角,若粒子的质量为m,电量为q,则(1)该粒子在磁场中作圆周运动的轨道半径为 ;(2)粒子在磁场中运动的时间为 ;(3)该粒子射出磁场的位置坐标为 。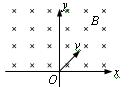
如图所示的坐标平面内,在y轴的左侧存在垂直纸面向外、磁感应强度大小B1=0.20T的匀强磁场,在y轴的右侧存在垂直纸面向里、宽度d=0.125m的匀强磁场B2.某时刻一质量m=2.0×10-8kg、电量q=+4.0×10-4C的带电微粒(重力可忽略不计),从x轴上坐标为(-0.25m,0)的P点以速度v=2.0×103 m/s沿y轴正方向运动.试求:
(1)微粒在y轴的左侧磁场中运动的轨道半径;
(2)微粒第一次经过y轴时速度方向与y轴正方向的夹角;
(3)要使微粒不能从右侧磁场边界飞出,B2应满足的条件
磁谱仪是测量α能谱的重要仪器。磁谱仪的工作原理如图所示,放射源S发出质量为m、电量为q的α粒子沿垂直磁场方向进入磁感应强度为B的匀强磁场,被限束光栏Q限制在2φ的小角度内,α粒子经磁场偏转后打到与束光栏平行的感光片P上。(重力影响不计)
⑴若能量在E~E+ΔE(ΔE>0,且 )范围内的α粒子均垂直于限束光栏的方向进入磁场。试求这些α粒子打在胶片上的范围Δx1。
)范围内的α粒子均垂直于限束光栏的方向进入磁场。试求这些α粒子打在胶片上的范围Δx1。
⑵实际上,限束光栏有一定的宽度,α粒子将在2φ角内进入磁场。试求能量均为E的α 粒子打到感光胶片上的范围Δx2 
如图所示,正方形容器处在匀强磁场中,一束电子从a孔垂直进入磁场射入容器中,其中一部分从c孔射出,一部分从d孔射出,则下列说法正确的是 ( )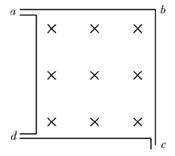
A.从两孔射出的电子速率之比为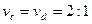 |
B.从两孔射出的电子在容器中运动所用时间之比为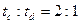 |
C.从两孔射出的电子在容器中运动时的加速度大小之比 |
D.从两孔射出的电子在容器中运动时的加速度大小之比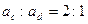 |
如右图所示,有界匀强磁场边界线SP//MN,速率不同的同种带电粒子(重力不计)从S 点沿SP方向同时射入磁场。其中穿过a点的粒子速度v1与MN垂直,穿过b点的粒子速度v2与MN成60°角,设两粒子从S到a、b所需时间分别为t1和t2。
(1)在图上画出两粒子的运动轨迹;
(2)求v1:v2;
(3)求t1:t2。
如图所示,NM的上侧有匀强磁场,磁场方向垂直于纸面向里,磁感应强度的大小为B。一带负电的粒子(不计重力)从P处以垂直于MN的初速度 射入磁场区域,最后通过
射入磁场区域,最后通过 点。已知此粒子的比荷
点。已知此粒子的比荷 ,求:
,求:
(1)P 间的距离L?
间的距离L?
(2)粒子从P运动到 需要多长的时间?
需要多长的时间?
如题图所示,在半径为a的圆柱空间中(图中圆为其横截面)充满磁感应强度大小为B的均匀磁场,其方向平行于轴线远离读者.在圆柱空间中垂直轴线平面内固定放置一绝缘材料制成的边长为L=1.6a的刚性等边三角形框架ΔDEF,其中心O位于圆柱的轴线上.DE边上S点( )处有一发射带电粒子的源,发射粒子的方向皆在图题图中截面内且垂直于DE边向下。发射粒子的电量皆为q(>0),质量皆为m,但速度v有各种不同的数值。若这些粒子与三角形框架的碰撞无能量损失,电量也无变化,且每一次碰撞时速度方向均垂直于被碰的边。试问:
)处有一发射带电粒子的源,发射粒子的方向皆在图题图中截面内且垂直于DE边向下。发射粒子的电量皆为q(>0),质量皆为m,但速度v有各种不同的数值。若这些粒子与三角形框架的碰撞无能量损失,电量也无变化,且每一次碰撞时速度方向均垂直于被碰的边。试问: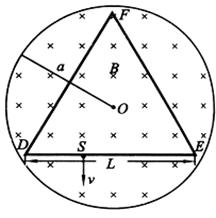
(1)带电粒子经多长时间第一次与DE边相碰?
(2)带电粒子速度v的大小取哪些数值时可使S点发出的粒子最终又回到S点?
(3)这些粒子中,回到S点所用的最短时间是多少?

如图,在区域内存在与
平面垂直的匀
 强磁场,磁感应强度的大小为
强磁场,磁感应强度的大小为.在
时刻,一位于坐标原点的粒子源在
平面内发射出大量同种带电粒子,所有粒子的初速度大小相同,方向与
轴正方向的
 夹角分布在
夹角分布在范围内。已知沿y轴正方向发射的粒子在
时刻刚好从磁场边界上
点离开磁场。求:
⑴ 粒子在磁场中做 圆周运动的半径
圆周运动的半径及粒子的比荷
;
⑵ 此时刻仍在磁场中的粒子的初速度方向与轴正方向夹角的取值范围;
⑶ 从粒子发射到全部粒子离开磁场所用的时间。
如图所示,在正三角形区域内存在着垂直于纸面的匀强磁场和平行于AB的水平方向的匀强电场,一不计重力的带电粒子刚好以某一初速度从三角形O点沿角分线OC做匀速直线运动。若此区域只存在电场时,该粒子仍以此初速度从O点沿角分线OC射入,则此粒子刚好从A点射出;若只存在磁场时,该粒子仍以此初速度从O点沿角分线OC射入,则下列说法正确的是:
| A.粒子将在磁场中做匀速圆周运动,运动轨道半径等于三角形的边长 |
| B.粒子将在磁场中做匀速圆周运动,且从OB阶段射出磁场 |
| C.粒子将在磁场中做匀速圆周运动,且从BC阶段射出磁场 |
| D.根据已知条件可以求出该粒子分别在只有电场时和只有磁场时在该区域中运动的时间之比 |
如图所示,直角三角形ABC区域中存在一匀强磁场,比荷相同的两个粒子沿AB方向射入磁场,
|
分别从AC边上的P、Q两点射出,则
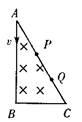
| A.从P射出的粒子速度大 |
| B.从Q射出的粒子速度大 |
| C.从P射出的粒子,在磁场中运动的时间长 |
| D.两粒子在磁场中运动的时间一样长 |
用磁聚焦法测比荷的装置如图所示.在真空玻璃管中装有热阴极K和带有小孔的阳极A.在A、K之间加上电压U后,不断地有电子从阴极K由静止加速到达阳极A,并从小孔射出.接着电子进入平行板电容器C,电容器两极板间加有不大的交变电场,使不同时刻通过的电子发生不同程度的偏转;电容器C和荧光屏S之间加一水平向右的均匀磁场,电容器和荧光屏间的距离为L,电子经过磁场后打在荧光屏上,将磁场的磁感应强度从零开始缓慢增大到为B时,荧光屏上的光点的锐度最大(这时荧光屏S上的亮斑最小).
(1)若平行板电容器C的板长为 ,求电子经过电容器和磁场区域的时间之比;
,求电子经过电容器和磁场区域的时间之比;
(2)用U、B、L表示出电子的比荷;
(3)在磁场区域再加一匀强电场,其电场强度的大小为 ,方向与磁场方向相反,若保持U、L和磁场方向不变,调节磁场的磁感应强度大小,仍使电子在荧光屏上聚焦,则磁感应强度大小满足的条件是什么?
,方向与磁场方向相反,若保持U、L和磁场方向不变,调节磁场的磁感应强度大小,仍使电子在荧光屏上聚焦,则磁感应强度大小满足的条件是什么?
大型强子对撞机是研究高能粒子的重要工具,同种物质的正反粒子由静止开始经电压为U的直线加速器加速后,沿切线方向进入对撞机的真空环状空腔内,空腔内存在与圆环平面垂直的匀强磁场,磁感应强度为B,两种粒子在环形空腔内沿相反方向作半径为r的匀速圆周运动,进而实现碰撞。下列说法正确的是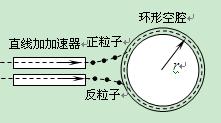
A.对于给定的加速电压,带电粒子的比荷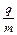 越大,磁感应强度B越大 越大,磁感应强度B越大 |
B.对于给定的加速电压,带电粒子的比荷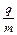 越大,磁感应强度B越小 越大,磁感应强度B越小 |
| C.对于给定的带电粒子,加速电压U越大,粒子运动的周期越大 |
| D.对于给定的带电粒子,不管加速电压U多大,粒子运动的周期都不变 |
如图所示,在内壁光滑、水平放置的玻璃圆环内,有一直径略小于环口径的带正电的小球,正以速率v0沿逆时针方向匀速转动.若在此空间突然加上方向竖直向上、磁感应强度B随时间成正比例增加的变化磁场,设运动过程中小球带的电荷量不变,那么( )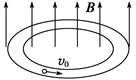
| A.磁场力对小球一直做正功 |
| B.小球受到的磁场力不断增大 |
| C.小球先沿逆时针方向做减速运动,过一段时间后,再沿顺时针方向做加速运动 |
| D.小球仍做匀速圆周运动 |
如图所示,在x<0与x >0的区域中,存在磁感应强度大小分别为B1与B2的匀强磁场,磁场方向均垂直于纸面向里,且B1>B2。一个带负电荷的粒子从坐标原点O以速度V沿x轴负方向射出,要使该粒子经过一段时间后又经过O点,B1与B2的比值应满足什么条件?
如图甲所示,在空心三棱柱CDF以外足够大的空间中,充满着磁感应强度为B的匀强磁场。三棱柱的轴线与磁场平行,截面边长为L,三棱柱用绝缘薄板材料制成,其内部有平行于CD侧面的金属板P、Q,两金属板间的距离为d,P板带正电,Q板带负电,Q板中心有一小孔,P板上与小孔正对的位置有一个粒子源S,从S处可以发出初速度为0、带电量为+q、质量为m的粒子,这些粒子与三棱柱侧面碰撞时无能量损失。试求:
(1)为使从S点发出的粒子最终又回到S点,P、Q之间的电压U应满足什么条件?(Q与CD之间距离不计)
(2)粒子从S点出发又回到S点的最短时间是多少?
(3)若磁场是半径为a的圆柱形区域,如图乙所示,圆柱的轴线与三棱柱的轴线重合,且a=( +
+ )L,要使S点发出的粒子最终又回到S点,则P、Q之间的电压不能超过多少?
)L,要使S点发出的粒子最终又回到S点,则P、Q之间的电压不能超过多少?