高中物理探究单摆的周期与摆长的关系试题

利用传感器和计算机可以测量快速变化的力的瞬时值。右图是用这种方法获得的弹性绳中拉力随时间的变化图线。实验时，把小球举高到绳子的悬点O处，然后放手让小球自由下落。由此图线所提供的信息，以下判断正确的是    。

A．t2时刻小球速度最大

B．t1～t2期间小球速度先增大后减小

C．t3时刻小球动能最小

D．t1与t4时刻小球动量一定相同

已知地面重力加速度大约是月面重力加速度的6倍。那么一台地面上的秒摆（运动周期为2.0秒）在月面上的运动周期约为     秒。（结果保留两位有效数字）

在做《用单摆测定重力加速度》的实验时，用摆长l和周期T计算重力加速度的公式是g=           。

做简谐振动的单摆摆长不变，把摆球质量增加为原来的4倍，使摆球经过平衡位置时的速度减小为原来的倍，则单摆振动的

A．周期、振幅都不变	B．周期不变、振幅减小
C．周期改变、振幅不变	D．周期、振幅都改变

一单摆做小角度摆动，其振动图象如图，以下说法正确的是

A．t1时刻摆球速度最大，悬线对它的拉力最小

B．t2时刻摆球速度最大，振动方向沿x正方向

C．t3时刻摆球速度为零，加速度最大，方向沿x负方向

D．t4时刻摆球速度最大，悬线对它的拉力最大

有一摆长为L的单摆，悬点正下方某处有一小钉，当摆球经过平衡位置向左摆动时，摆线的上部将被小钉挡住，使摆长发生变化，现使摆球做小幅度摆动，摆球从右边最高点M至左边最高点N运动过程的闪光照片如右图所示，(悬点和小钉未被摄入)，P为摆动中的最低点。已知每相邻两次闪光的时间间隔相等，由此可知，小钉与悬点的距离为(    )

A．3L/4

B．L/2

C．L/4

D．无法确定

如图12－1－9甲所示是一个单摆振动的情形，O是它的平衡位置，B、C是摆球所能到达的最远位置．设摆球向右方向运动为正方向．图乙所示是这个单摆的振动图象．根据图象回答：(取π²＝10)

(1)单摆振动的频率是多大？
(2)开始时刻摆球在何位置？
(3)若当地的重力加速度为10 m/s²，试求这个摆的摆长是多少？

如图12－1－6所示，一个光滑的圆弧形槽半径为R，放在水平地面上，圆弧所对的圆心角小于5°.AD的长为x，今有一小球m₁以沿AD方向的初速度v从A点开始运动，要使小球m₁可以与固定在D点的小球m₂相碰撞，那么小球m₁的速度v应满足什么条件？

有人利用安装在气球载人舱内的单摆来确定气球的高度．已知该单摆在海平面处的周期是T₀.当气球停在某一高度时，测得该单摆周期为T.求该气球此时离海平面的高度h.(把地球看做质量均匀分布的半径为R的球体)

在用单摆测重力加速度的实验中同学在实验中，先测得摆线长为97.50cm，再测得摆球直径为2.00cm，然后测出了单摆全振动50次所用时间为98.0s，
（1）该单摆的摆长为      cm，周期为      s。
（2）如果他测得的g值偏小，可能原因是________

A．测摆线长时将摆线拉得过紧	B．误将摆线长当作摆长
C．开始计时，秒表按下偏迟	D．实验中误将49次全振动计为50次

在“探究单摆摆长与周期关系”的实验中，某同学的主要操作步骤如下：
A．取一根符合实验要求的摆线，下端系一金属小球，上端固定在O点；
B．在小球静止悬挂时测量出O点到小球球心的距离l；
C．拉动小球使细线偏离竖直方向一个不大的角度（约为5°），然后由静止释放小球；
D．用秒表记录小球完成n次全振动所用的时间t。
①用所测物理量的符号表示重力加速度的测量值，其表达式为g=         ；
②若测得的重力加速度数值大于当地的重力加速度的实际值，造成这一情况的原因可能是       
（选填下列选项前的序号）
A、测量摆长时，把摆线的长度当成了摆长
B、摆线上端未牢固地固定于O点，振动中出现松动，使摆线越摆越长
C、测量周期时，误将摆球（n-1）次全振动的时间t记为了n次全振动的时间，并由计算式T=t/n求得周期
D、摆球的质量过大
③在与其他同学交流实验方案并纠正了错误后，为了减小实验误差，他决定用图象法处理数据，并通过改变摆长，测得了多组摆长l和对应的周期T，并用这些数据作出T²-l图象如图甲所示。若图线的斜率为k，则重力加速度的测量值g=       。

④这位同学查阅资料得知，单摆在最大摆角q较大时周期公式可近似表述为。为了用图象法验证单摆周期T和最大摆角q的关系，他测出摆长为l的同一单摆在不同最大摆角q时的周期T，并根据实验数据描绘出如图乙所示的图线。根据周期公式可知，图乙中的纵轴表示的是           ，图线延长后与横轴交点的横坐标为          。

如图甲是一个单摆振动的情形，O是它的平衡位置，B、C是摆球所能到达的最远位置．设摆球向右运动为正方向．图乙是这个单摆的振动图象．根据图象回答：

(1)单摆振动的频率是多大？
(2)开始时刻摆球在何位置？
(3)若当地的重力加速度为10 m/s²，这个摆的摆长是多少？

如图所示，一单摆悬于O点，摆长为L，若在O点的竖直线上的O′点钉一个钉子，使OO′＝L/2，将单摆拉至A处释放，小球将在A、B、C间来回振动，若振动中摆线与竖直方向夹角小于10°，则此摆的周期是(　　)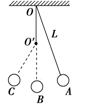

A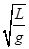．2π                         B．2π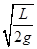
C．2π(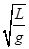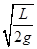＋ )               D．π(＋ )

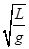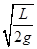做简谐振动的单摆摆长不变，若摆球质量增加为原来的4倍，摆球经过平衡位置时速度减小为原来的1/2，则单摆振动的(　　)

A．频率、振幅都不变	B．频率、振幅都改变
C．频率不变，振幅改变	D．频率改变，振幅不变

做简谐振动的单摆，在摆动的过程中(　　)

A．只有在平衡位置时，回复力才等于重力和细绳拉力的合力

B．只有在最高点时，回复力才等于重力和细绳拉力的合力

C．小球在任意位置处，回复力都等于重力和细绳拉力的合力

D．小球在任意位置处，回复力都不等于重力和细绳拉力的合力