高中物理探究单摆的周期与摆长的关系试题

如图所示，将小球甲、乙、丙（都可视为质点）分别从A、B、C三点由静止同时释放，最后都到达竖直面内圆弧的最低点D，其中甲是从圆心A出发做自由落体运动，乙沿弦轨道从一端B到达另一端D，丙沿圆弧轨道从C点运动D，且C点很靠近D点。如果忽略一切摩擦阻力，那么下列判断正确的是：(      ) 
  
A．甲球最先到达D点，乙球最后到达D点
B．甲球最先到达D点，丙球最后到达D点
C．丙球最先到达D点，乙球最后到达D点
D．甲球最先到达D点，无法判断哪个球最后到达D点

摆长为L的单摆做简谐运动，若从某时刻开始计时(取t＝0)，当振动至t＝ 时，摆球具有负向最大速度，则单摆的振动图象是图中的  (　    　)

如图所示，用两根长度都为l的细线悬挂一个小球A，两悬挂点等高，线与水平天花板间的夹角都是α，使球A在垂直于纸面的平面内做小幅度的摆动，当A经过平衡位置的瞬间，另一小球B从A球的正上方自由下落，若B球恰能击中A球，求B球开始下落时离A球振动平衡位置的高度。

有两个单摆做简谐运动，位移与时间关系是：x₁=3asin(4πbt+)和x₂=9asin(8πbt+)，其中a、b为正的常数，则它们的：振幅之比为__________；摆长之比为_________。

一个单摆在甲地时，在时间t内完成m次全振动，移至乙地时，经过相同的时间完成n次全振动，则甲、乙两地重力加速度大小之比g_甲：g_乙等于______________。

某同学在用单摆测定重力加速度的实验中，测量不同摆长情况下单摆的振动周期，并以L为横坐标，为纵坐标，做出了图线，如图所示，由此图线可知重力加速度为            m/s²。　　　　　　　　　　　　　　　　　　　

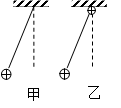
如右图甲所示，有一质量为m、带电量为+q的小球在竖直平面内做单摆，摆长为L，当地的重力加速度为g，则周期T=        ；若在悬点处放一带正电的小球（图乙），则周期将        。（填“变大”、“不变”、“变小”）

一个单摆的振动周期是2s，求下列作简谐运动情况下单摆的周期：
（1）摆长缩短为原来的1/4，单摆的周期为________s；
（2）摆球的质量减为原来的1/4，单摆的周期为________s；
（3）振幅减为原来的1/4，单摆的周期为________s。

两个摆长相同的单摆，摆球质量之比是4:1，在不同地域振动，当甲摆振动4次的同时，乙摆恰振动5次，则甲、乙二摆所在地区重力加速度之比为             。

下图甲是一个单摆振动的情形，O是它的平衡位置，B、C是摆球所能到达的最远位置，设摆球向右方向运动为正方向，下图乙是这个单摆的振动图象，根据图象回答：

(1)单摆振动的频率是多大？
(2)开始时刻摆球在何位置？
(3)若当地的重力加速度为9.86 m/s²， 试求这个摆的摆长是多少？

一单摆的摆长为40cm，摆球在t=0时刻正从平衡位置向右运动，若g取10 m／s²，则在1s时摆球的运动情况是 ：

A．正向左做减速运动，加速度正在增大	B．正向左做加速运动，加速度正在减小
C．正向右做减速运动，加速度正在增大	D．正向右做加速运动，加速度正在减小

如图所示，两个单摆A和B，其摆长L_A＞L_B，将它们都拉离竖直方向一个很小的角度，然后由静止释放，那么两个球到达最低点时的速度大小与经历时间关系的多少为()

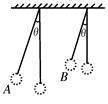
A．vA＞vB，tA＞tB	B．vA＜vB，tA＜tB
C．vA＞vB，tA＜tB	D．vA＜vB，tA＞tB

如图所示的实线和虚线分别表示同一个单摆在A、B两个星球半径大小相同的星球表面上的振动图象，其中实线是A星球上的，虚线是B星球上的，那么两个星球的平均密度ρ_A和ρ_B之比是__________。

如右图甲所示，有一质量为m、带电量为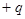的小球在竖直平面内做单摆，摆长为L，当地的重力加速度为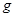，则周期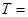        ；若在悬点处放一带正电的小球（图乙），则周期将        。（填“变大”、“不变”、“变小”）

如图所示，半径是0.2m的圆弧状光滑轨道置于竖直面内并固定在地面上，轨道的最低点为B，在轨道的A点（弧AB所对圆心角小于5°）和弧形轨道的圆心O两处各有一个静止的小球Ⅰ和Ⅱ，若将它们同时无初速释放，先到达B点的是________球