以 的两边 、 为边，向外作正方形 和正方形 ，连接 ，过点 作 于 ，延长 交 于点 ．
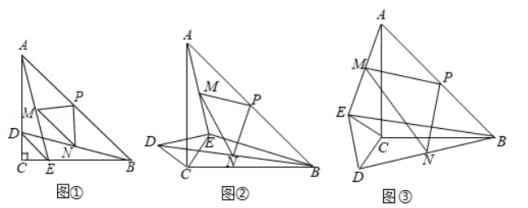
（ 1 ）如图 1 ，若 ， ，易证： ；
（ 2 ）如图 2 ， ；如图 3 ， ，（ 1 ）中结论，是否成立，若成立，选择一个图形进行证明；若不成立，写出你的结论，并说明理由．
相关试题
（每小题6分，共12分）
（1）先化简，再求值: [（2x-3y）2-2x（2x+3y）]÷9y，其中x=3，y=-2．
（2）已知a+b=4，ab=3，求（a-b）2的值．
如图，在等边△ABC中， M为BC边上的中点， D是射线AM上的一个动点，以CD为一边且在CD的下方作等边△CDE，连接BE．
（1）填空：若D与M重合时（如图1）∠CBE= 60°度；
（2）如图2，当点D在线段AM上时（点D不与A、M重合），请判断（1）中结论是否成立？并说明理由；
（3）在（2）的条件下，如图3，若点P、Q在BE的延长线上，且CP=CQ=4，AB=6，试求PQ的长．
某服装店用6000元购进A，B两种新式服装，按标价售出后可获得毛利润3800元（毛利润=售价－进价），这两种服装的进价、标价如下表所示：
| 类型 价格 |
A型 |
B型 |
| 进价（元/件） |
60 |
100 |
| 标价（元/件） |
100 |
160 |
（1）求这两种服装各购进的件数；
（2）如果A中服装按标价的8折出售，B中服装按标价的7折出售，那么这批服装全部售完后，服装店比按标价售出少收入多少元？
，
，求代数式
的值．
粤公网安备 44130202000953号