如图,已知三棱柱 ABC- A 1 B 1 C 1的底面是正三角形,侧面 BB 1 C 1 C是矩形, M, N分别为 BC, B 1 C 1的中点, P为 AM上一点.过 B 1 C 1和 P的平面交 AB于 E,交 AC于 F.
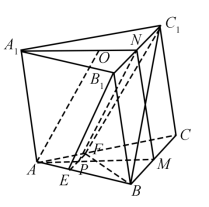
(1)证明: AA 1// MN,且平面 A 1 AMN⊥平面 EB 1 C 1 F;
(2)设 O为△ A 1 B 1 C 1的中心,若 AO= AB=6, AO//平面 EB 1 C 1 F,且∠ MPN= ,求四棱锥 B- EB 1 C 1 F的体积.
推荐套卷
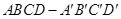 中,
中,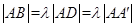 ,(
,(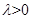 ),
),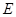 、
、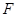 分别是
分别是 和
和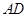 的中点,且
的中点,且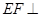 平面
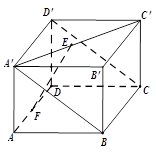
平面 .
.
 的值;
的值;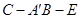 的余弦值.
的余弦值.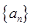 的前
的前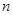 项和为
项和为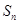 ,且满足
,且满足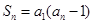 .
.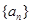 的通项公式;
的通项公式;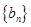 满足
满足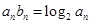 ,求数列
,求数列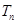 .
.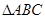 的三个内角A、B、C的对边分别为
的三个内角A、B、C的对边分别为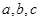 ,且
,且 .
.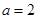 ,且
,且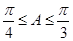 ,求边
,求边 的取值范围.
的取值范围. ,求
,求 的取值范围;
的取值范围;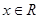 ,
, 恒成立,求
恒成立,求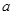 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号