直播购物逐渐走进了人们的生活.某电商在抖音上对一款成本价为40元的小商品进行直播销售,如果按每件60元销售,每天可卖出20件.通过市场调查发现,每件小商品售价每降低5元,日销售量增加10件.
(1)若日利润保持不变,商家想尽快销售完该款商品,每件售价应定为多少元?
(2)小明的线下实体商店也销售同款小商品,标价为每件62.5元.为提高市场竞争力,促进线下销售,小明决定对该商品实行打折销售,使其销售价格不超过(1)中的售价,则该商品至少需打几折销售?
相关知识点
推荐套卷
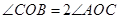 ,
,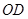 平分
平分 ,且
,且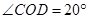 ,求
,求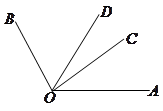
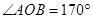 ,
, ,
,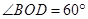 ,求
,求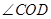 的大小.
的大小.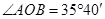 ,
, ,
,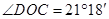 ,
,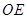 平分
平分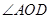 ,求
,求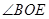 的度数.
的度数.
 是直线
是直线 上的点,
上的点,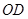 是
是 的平分线,
的平分线,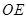 是
是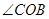 的平分线,求
的平分线,求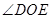 的度数.
的度数.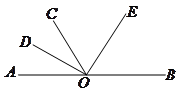
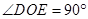 ,
,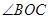 ?
? ,
,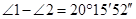 ,且
,且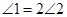 ,求
,求 和
和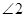 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号